- ... tensiones1.1
- En mecánica de fluidos no
suele utilizarse el término ``esfuerzo'' con el sentido que se le
da en otras áreas de la mecánica de medios continuos, y muy
frecuentemente se emplea ``esfuerzo'' para designar el concepto de
``tensión''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... éste.1.2
- Un sólido
apoyado en el suelo, en el que, en ausencia de otras fuerzas
distintas de la fuerza gravitatoria, existen tensiones cortantes,
se deforma y adopta una forma que permanece constante mientras no
se modifiquen las fuerzas que actúan sobre el cuerpo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sean.1.3
- Si
se eliminan súbitamente las paredes de un recipiente que contenga
un líquido inicialmente en reposo (sometido por tanto a tensiones
normales exclusivamente) bajo la acción de la gravedad, se
producirá un desequilibro que dará lugar a la aparición de
tensiones cortantes y a una deformación continua que provocará el
derramamiento del líquido.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
condiciones1.4
- El flujo que se está describiendo es el
llamado flujo de Couette, en el que los efectos de la viscosidad
son dominantes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... libre1.5
- El concepto de
superficie libre se comenta brevemente en una nota al pie de la
página
![[*]](crossref.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... hipótesis1.6
- La hipótesis de
medio continuo parece intuitivamente razonable pero, en vista del
carácter discontinuo de la materia, constituida por átomos y
moléculas, debe justificarse.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inercia1.7
- Las
fuerzas de inercia son debidas al movimiento no inercial del
sistema de referencia. En el flujo en grandes escalas que tiene
lugar en la atmósfera, por ejemplo, no pueden despreciarse las
fuerzas de Coriolis debidas al movimiento de rotación de la
tierra. Sin embargo, generalmente la tierra puede considerarse un
sistema de referencia inercial.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....1.8
-
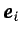 es el vector unitario según
la dirección del eje
es el vector unitario según
la dirección del eje 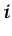 de coordenadas.
de coordenadas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... principal,1.9
- Una
propiedad de los tensores de segundo orden consiste en que la
suma de las tres componentes de la diagonal principal permanece
invariante en cualquier sistema de referencia ortogonal; es decir,
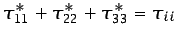 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
pequeño.1.10
- El equilibrio termodinámico se establece
mediante choques entre moléculas, y la hipótesis de equilibrio
termodinámico local está justificada si la distancia típica de
variación de las magnitudes fluidas es mucho mayor que el
recorrido libre medio de las moléculas, como ocurre en la inmensa
mayoría de los problemas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... estado:1.11
- La ecuación (1.11) suele
denominarse a veces ecuación de estado térmica. Cuando la variable
dependiente es una de las llamadas variables de estado calóricas
(tales como energía interna, entalpía o entropía), la
correspondiente ecuación se denomina ecuación de estado calórica
(p. ej., ecuación (1.12)).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... densidad:1.12
- Puede demostrarse
que la ecuación (1.20) implica que la energía interna sólo
depende de la temperatura.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Fourier:1.13
- En la referencia
de Batchelor (1967), por ejemplo, pueden encontrarse argumentos en
favor de la hipótesis de dependencia lineal entre el vector flujo
de calor por unidad de área y el gradiente local de la
temperatura. Este tipo de dependencia se introducirá también en
las secciones siguientes para describir el transporte de masa por
difusión y, para el caso de un flujo con una distribución muy
simple de velocidad, el de cantidad de movimiento.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
tensor1.14
- Tanto
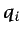 como
como
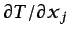 son
componentes de sendos vectores, y dado que la ecuación
(1.32) es válida en cualquier sistema de coordenadas,
son
componentes de sendos vectores, y dado que la ecuación
(1.32) es válida en cualquier sistema de coordenadas,
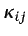 debe ser la componente
debe ser la componente 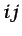 de un tensor de segundo
orden.
de un tensor de segundo
orden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
suavizarla.1.15
- La variación espacial de la temperatura
produce un flujo de calor que da lugar a la transmisión de calor
desde las zonas que se encuentran a mayor temperatura hacia las
zonas más frías. La variación espacial de velocidad genera fuerzas
de superficie (flujo de cantidad de movimiento desde las regiones
del flujo donde la velocidad es mayor hacia las de menor
velocidad) que tienden a frenar el fluido con mayor velocidad y a
acelerar el fluido más lento.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fluida,2.1
- Cada partícula fluida
(formada siempre por una determinada porción de fluido) debe
permanecer identificable en todo instante, y dado que puede sufrir
deformaciones en su movimiento, sus dimensiones lineales deben
permanecer suficientemente pequeñas, lo que se garantiza en todo
caso idealizándola y considerándola como un punto material.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
escribirse2.2
- En la descripción que se está haciendo, no se
admite la posibilidad de que una partícula fluida se divida y
llegue a ocupar dos posiciones, ni que dos partículas fluidas
ocupen la misma posición simultáneamente. Por otra parte, la
continuidad del movimiento requiere que una ``cadena'' formada en
un instante dado por un conjunto de partículas fluidas contiguas,
denominada línea fluida, no se ``rompa'', y evolucione de
forma que las partículas sigan formando la misma línea fluida en
todo momento. Estas condiciones requieren que la función de la
ecuación (2.1) sea continua y no múltiple, y que pueda
invertirse para poder obtener la ecuación (2.2), en la que
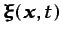 es también una función continua y no
múltiple. Una condición necesaria y suficiente para que la función
inversa exista es que el Jacobiano
es también una función continua y no
múltiple. Una condición necesaria y suficiente para que la función
inversa exista es que el Jacobiano
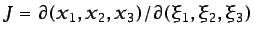 sea no
nulo.
sea no
nulo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...tray2):2.3
- La ecuación (2.3) expresa que el
valor de la propiedad
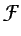 en la posición
en la posición 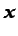 e
instante
e
instante 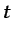 coincide con el valor de la propiedad en la partícula
fluida que está en
coincide con el valor de la propiedad en la partícula
fluida que está en 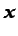 en el instante
en el instante 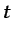 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...tray):2.4
- La ecuación
(2.4) expresa que el valor de la propiedad
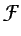 en la partícula fluida en el instante
en la partícula fluida en el instante 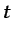 coincide con el valor de
coincide con el valor de
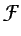 en la posición que ocupa la partícula en dicho
instante.
en la posición que ocupa la partícula en dicho
instante.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
euleriana.2.5
- En algunos problemas (por ejemplo, en algunos
flujos interfaciales) puede ser conveniente un enfoque lagrangiano
o de tipo mixto.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
bidimensional:2.6
- No siempre se hace esta distinción entre
flujos bidimensionales y planos.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... axilsimétricos,2.7
- Algunos autores denominan
también axilsimétricos a flujos en los que existe una componente
acimutal de la velocidad que no depende de la coordenada
acimutal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... demostrar2.8
- Véase, por ejemplo, Aris (1962).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... demostrarse2.9
- Véase, por ejemplo,
Crespo (1997).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... interpretarse2.10
- Véase la
discusión sobre la Figura 1.1 para el flujo simple
considerado en ella.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cerrada2.11
- Recuérdese que una
línea fluida está formada en todo instante por las mismas
partículas fluidas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... potencial,2.12
- Véase la Sección
5.3.4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fluida3.1
- Las definiciones de superficie fluida y
volumen fluido son análogas a la de línea fluida (véase la nota al
pie de la página
![[*]](crossref.gif) ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
fluidas.3.2
- Análogamente a como una partícula fluida
(``punto material'') está siempre formada por las ``mismas
moléculas''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... magnitud3.3
- La energía interna
y la cantidad de movimiento en los dos ejemplos citados.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... deducir,3.4
- Puede consultarse
Crespo (1997) o, para una deducción más detallada, Aris (1962).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Gauss,3.5
- Se le suele denominar
también teorema de Green, de Gauss-Ostrogradsky o de la
divergencia.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... incompresible,3.6
- En numerosos problemas de
interés, un gas puede comportarse como incompresible. Por otra
parte, los efectos de compresibilidad en líquidos deben ser
tenidos en cuenta en ciertas ocasiones; por ejemplo, en flujos no
estacionarios en conductos en los que se producen aperturas o
cierres bruscos de válvulas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
total,3.7
- En general, las ecuaciones de conservación de la
masa y de las fracciones másicas de
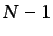 especies deberán ser
resueltas junto con las ecuaciones de conservación de la cantidad
de movimiento y de la energía que se describen en las siguientes
secciones.
especies deberán ser
resueltas junto con las ecuaciones de conservación de la cantidad
de movimiento y de la energía que se describen en las siguientes
secciones.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... orden.3.8
-
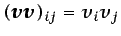 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...).3.9
- La ecuación (3.29)
permite dar una interpretación intuitiva, poco rigurosa, al
coeficiente
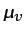 . La presión en un gas es debida a la velocidad
de agitación de las moléculas, y cuando se comprime una cierta
masa de gas se consigue aumentar la presión al aumentar la energía
asociada a dicha velocidad de agitación. No obstante, en general la
energía interna del gas no sólo se debe a la velocidad de
agitación, sino que también está asociada a otros grados de
libertad como la rotación y la vibración de las moléculas. Al
aumentar la presión sobre el gas, el consiguiente aumento de la
energía interna debida a la velocidad de agitación se
transfiere en parte, mediante choques entre moléculas, a los otros
grados de libertad, hasta que se alcance el equilibrio. Cuando la
compresión es muy rápida (en la Sección 2.4 se explicó
que
. La presión en un gas es debida a la velocidad
de agitación de las moléculas, y cuando se comprime una cierta
masa de gas se consigue aumentar la presión al aumentar la energía
asociada a dicha velocidad de agitación. No obstante, en general la
energía interna del gas no sólo se debe a la velocidad de
agitación, sino que también está asociada a otros grados de
libertad como la rotación y la vibración de las moléculas. Al
aumentar la presión sobre el gas, el consiguiente aumento de la
energía interna debida a la velocidad de agitación se
transfiere en parte, mediante choques entre moléculas, a los otros
grados de libertad, hasta que se alcance el equilibrio. Cuando la
compresión es muy rápida (en la Sección 2.4 se explicó
que
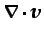 es la velocidad de dilatación
cúbica unitaria), el tiempo empleado en alcanzarse el equilibrio
(es decir, en producirse la repartición de energía de agitación de
las moléculas entre los diferentes grados de libertad) puede
llegar a ser suficientemente grande frente al tiempo de
compresión, de forma que la presión mecánica llega a ser mayor que
la presión termodinámica que correspondería a un estado de
equilibrio. En gases monoatómicos, la energía de las moléculas es
exclusivamente debida al movimiento de agitación y no se produce,
por tanto, el mecanismo de repartición de energía interna entre
diferentes grados de libertad (que no existen), de forma que
es la velocidad de dilatación
cúbica unitaria), el tiempo empleado en alcanzarse el equilibrio
(es decir, en producirse la repartición de energía de agitación de
las moléculas entre los diferentes grados de libertad) puede
llegar a ser suficientemente grande frente al tiempo de
compresión, de forma que la presión mecánica llega a ser mayor que
la presión termodinámica que correspondería a un estado de
equilibrio. En gases monoatómicos, la energía de las moléculas es
exclusivamente debida al movimiento de agitación y no se produce,
por tanto, el mecanismo de repartición de energía interna entre
diferentes grados de libertad (que no existen), de forma que
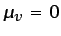 y, por tanto,
y, por tanto, 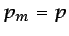 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sigue:3.10
-
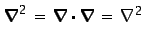 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
viscosidad).3.11
- Esto no significa que las tensiones debidas
a la viscosidad tengan que ser nulas, sino que no dan lugar a una
fuerza resultante sobre la partícula fluida.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
identidad3.12
-
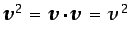 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
siguiente:3.13
- Recuérdese que esta ecuación se ha obtenido
suponiendo que la densidad y la viscosidad son constantes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (interna+ci\-né\-ti\-ca)3.14
- Se
prescindirá de la energía de formación en la energía interna. Las
variaciones de energía interna debidas a reacciones químicas se
tratarán mediante la introducción de una aportación adicional
externa de calor.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ecuaciones3.15
- Existiría otra
ecuación análoga para
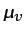 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... temperatura3.16
- Los dos últimos efectos
mencionados (no así los efectos no newtonianos en numerosas
aplicaciones de interés), suelen ser despreciables en la inmensa
mayoría de las aplicaciones prácticas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fluidodinámicos.3.17
- En esta sección
se hace referencia a algunos conceptos que se tratarán en el
Capítulo 5.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
periódica,3.18
- Cuando el flujo es turbulento, entenderemos
que la solución es estacionaria si las magnitudes promediadas se
mantienen constantes en el tiempo. En este tipo de flujos, como se
explicará en la Sección 5.4.5, las magnitudes
instantáneas en cada punto varían en el tiempo de forma
aparentemente aleatoria a pesar de que las condiciones de contorno
sean en principio estacionarias.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... iniciales.3.19
- No obstante, en la resolución
numérica de problemas estacionarios, frecuentemente se introduce
en las ecuaciones un término ficticio no estacionario, y se parte
de una solución inicial que ``evoluciona'' hasta converger a la
solución estacionaria buscada, a la vez que el término no
estacionario va reduciéndose progresivamente hasta hacerse
despreciable.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pared,3.20
- La condición de adherencia no se
satisface en gases con muy baja densidad, en los que la velocidad
media de las moléculas varía apreciablemente en distancias del
orden del recorrido libre medio de las moléculas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... relevante,3.21
- Por razones de espacio, no se
han tratado en capítulos previos, y tampoco siquiera mencionado,
los fenómenos de tensión superficial. En los textos de
Liñán (1967); Crespo (1997); Batchelor (1967), por ejemplo, puede encontrarse una
introducción al tema.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... perfecto4.1
- El análisis que
se hace es válido también para flujos de fluidos incompresibles,
para los que habría que simplificar las ecuaciones según se indicó
en el capítulo anterior. En particular, como ya se ha mencionado,
las ecuaciones de conservación de la masa y de la cantidad de
movimiento quedarían desacopladas si la viscosidad no depende de
la temperatura, y obviamente no debe utilizarse la ecuación
(4.4).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
conocidos4.2
- Los parámetros indicados pueden aparecer
directamente en las ecuaciones (por ejemplo,
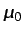 , tanto si la
viscosidad del fluido es constante e igual a
, tanto si la
viscosidad del fluido es constante e igual a 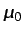 , como si, por
ejemplo, depende sólo de la temperatura y
, como si, por
ejemplo, depende sólo de la temperatura y 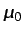 es un valor de
la viscosidad a una temperatura de referencia), o en las
condiciones iniciales y de contorno (
es un valor de
la viscosidad a una temperatura de referencia), o en las
condiciones iniciales y de contorno (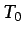 puede ser la
temperatura inicial del fluido,
puede ser la
temperatura inicial del fluido, 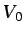 puede ser la velocidad del
fluido entrante en el dominio considerado a través de una
determinada sección y
puede ser la velocidad del
fluido entrante en el dominio considerado a través de una
determinada sección y 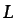 puede ser una longitud característica
del problema).
puede ser una longitud característica
del problema).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
quasi-estacionario.4.3
- Por ejemplo, en el vaciado de un
depósito de grandes dimensiones a través de un orificio de
dimensiones muy pequeñas, el caudal o flujo másico de salida puede
determinarse en cada instante a partir de ecuaciones en las que se
ha despreciado el término no estacionario. Esta aproximación es
compatible con el hecho de que la altura de la superficie libre
del líquido o la densidad del gas en el depósito, según sea el
caso, varíen en el tiempo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....4.4
- En el vaciado del líquido contenido en un
depósito a través de un orificio, el tiempo característico del
problema es el de vaciado del depósito y la longitud
característica es la que recorre una partícula fluida sometida a
aceleración apreciable. Esta longitud característica vendrá dada
por el tamaño de la zona en torno al orificio en la que la
velocidad del líquido puede considerarse apreciable, el cual,
teniendo en cuenta la ecuación de continuidad, se deduce que será
del orden del tamaño del orificio. El tiempo que tarda una
partícula fluida en pasar por la mencionada zona se denomina
tiempo de residencia,
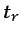 . Es fácil demostrar que la condición
de quasi-estacionareidad
. Es fácil demostrar que la condición
de quasi-estacionareidad
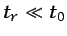 es equivalente a la
condición (que no contradice la intuición) de que el volumen de
líquido en el depósito sea mucho mayor que el de la zona de
aceleración descrita.
es equivalente a la
condición (que no contradice la intuición) de que el volumen de
líquido en el depósito sea mucho mayor que el de la zona de
aceleración descrita.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... superiores,4.5
- Algunos valores
típicos de Re:
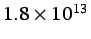 en la capa límite terrestre
(
en la capa límite terrestre
(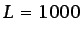 km,
km, 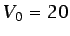 m/s);
m/s);
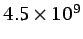 en el flujo
alrededor de barcos transatlánticos (
en el flujo
alrededor de barcos transatlánticos (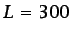 m,
m, 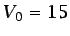 m/s);
m/s);
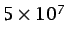 en el flujo alrededor de un avión comercial de
pasajeros a altitud de crucero;
en el flujo alrededor de un avión comercial de
pasajeros a altitud de crucero;
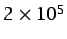 en el flujo
alrededor de una pelota de tenis a más de 100 km/h; 1 en el flujo
de aire alrededor de una gota de agua de 0.1 mm cayendo bajo la
acción de la gravedad; en biología, por ejemplo, es posible
encontrar numerosos flujos en los que Re es mucho menor que la
unidad.
en el flujo
alrededor de una pelota de tenis a más de 100 km/h; 1 en el flujo
de aire alrededor de una gota de agua de 0.1 mm cayendo bajo la
acción de la gravedad; en biología, por ejemplo, es posible
encontrar numerosos flujos en los que Re es mucho menor que la
unidad.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... libre4.6
- Los flujos
con superficie libre son casos particulares de flujos
interfaciales, en los que uno de los fluidos (generalmente un gas)
tiene una influencia despreciable en la dinámica del problema.
Esto permite simplificar el tratamiento de una de las fases. Un
ejemplo puede ser el movimiento de un líquido en el interior de un
depósito parcialmente lleno, en el que existe un gas por encima de
la superficie libre. Es generalmente aceptable suponer que en el
gas la presión es uniforme en cada instante y la viscosidad
despreciable.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
flujo.4.7
- El número de Mach se ha definido en la ecuación
(4.19) a partir de parámetros característicos del problema,
pero también puede definirse localmente a partir de las
velocidades del fluido y de propagación del sonido en cada punto
del campo fluido. Análogamente ocurre con otros números
adimensionales. La variación del valor de un número adimensional
en el campo fluido puede determinar que el carácter del flujo sea
diferente de unas zonas a otras, como se comentará más adelante.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... masa4.8
- A la difusividad de masa
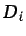 se la
denominó anteriormente coeficiente de difusión.
se la
denominó anteriormente coeficiente de difusión.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,4.9
- Los tres últimos aparecen cuando los
efectos de propiedades variables son relevantes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... simplificados5.1
- En el desarrollo de
estos modelos simplificados una herramienta matemática muy
importante la constituyen los métodos de perturbaciones, basados
en la utilización de expansiones asintóticas para analizar el
comportamiento de la solución de un sistema de ecuaciones
diferenciales cuando se hace tender a cero un parámetro (o
parámetros) arbitrariamente pequeño (
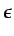 ) que aparece en
las ecuaciones. En general, puede hablarse de dos tipos de
enfoques. En el primero se utilizan métodos (de perturbaciones
regulares) que, en determinados problemas, permiten obtener una
única solución uniformemente válida (la solución perturbada
converge uniformemente hacia la solución de la ecuación
simplificada obtenida haciendo
) que aparece en
las ecuaciones. En general, puede hablarse de dos tipos de
enfoques. En el primero se utilizan métodos (de perturbaciones
regulares) que, en determinados problemas, permiten obtener una
única solución uniformemente válida (la solución perturbada
converge uniformemente hacia la solución de la ecuación
simplificada obtenida haciendo
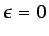 ). Sin embargo, estos
métodos no son aplicables en problemas en los que el orden de las
ecuaciones diferenciales completas es superior al de las
ecuaciones simplificadas. Esto se debe a que la eliminación de los
términos que contienen las derivadas de mayor orden hace que la
solución de las ecuaciones aproximadas no satisfaga determinadas
condiciones de contorno. En tales casos se utilizan métodos de
perturbaciones singulares, que permiten obtener soluciones
uniformemente válidas en regiones diferentes que se solapan en un
cierto grado. Estas soluciones pueden ser acopladas en las zonas
de solapamiento mediante la elección de constantes de integración
apropiadas.
). Sin embargo, estos
métodos no son aplicables en problemas en los que el orden de las
ecuaciones diferenciales completas es superior al de las
ecuaciones simplificadas. Esto se debe a que la eliminación de los
términos que contienen las derivadas de mayor orden hace que la
solución de las ecuaciones aproximadas no satisfaga determinadas
condiciones de contorno. En tales casos se utilizan métodos de
perturbaciones singulares, que permiten obtener soluciones
uniformemente válidas en regiones diferentes que se solapan en un
cierto grado. Estas soluciones pueden ser acopladas en las zonas
de solapamiento mediante la elección de constantes de integración
apropiadas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sigue:5.2
- Recuérdese que la ecuación
(3.36) se dedujo suponiendo uniformes los
coeficientes de viscosidad.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... satisface5.3
- Véase la ecuación
(3.44).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nula.5.4
- A pesar de lo indicado, conviene precisar
que, salvo en algunos casos triviales, la irrotacionalidad del
flujo requiere generalmente que el fluido pueda considerarse
ideal. Para ello, al menos uno de los números adimensionales Re o
(Re)(St) debe ser mucho mayor que la unidad (véase la Sección
5.4.4), si bien, aun en este caso, existirán inevitablemente
en el campo fluido zonas de vorticidad no nula (en capas límite y
estelas, y aguas abajo de ondas de choque curvas). Véase el texto
de Liñán (1967).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
por5.5
- Obsérvese que, introduciendo las ecuaciones
(5.16) y (5.17) en la ecuación (5.15),
resulta
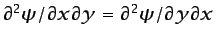 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
longitud5.6
- Volumen de fluido por unidad de longitud y de
tiempo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... complejo.5.7
- La notación empleada (letras
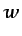 y
y
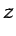 ) es la habitual, y en este contexto no deben dar lugar a
confusión con otras magnitudes.
) es la habitual, y en este contexto no deben dar lugar a
confusión con otras magnitudes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... siguiente:5.8
- Obsérvese que
d
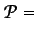 d
d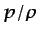 es una diferencial exacta.
es una diferencial exacta.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... movimiento,5.9
- Veremos más
adelante en qué circunstancias ocurre esto.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... justificación5.10
- En la Sección
5.4.7 se hacen algunos comentarios breves sobre esta
cuestión.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... adimensional).5.11
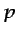 se ha redefinido como presión
reducida (véase la ecuación (5.42).
se ha redefinido como presión
reducida (véase la ecuación (5.42).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...wphi-4),5.12
- Se ha
preferido deducir de nuevo aquí esta ecuación, directamente a
partir de las correspondiente ecuaciones de Navier-Stokes ya
simplificadas, en lugar de simplificar una forma más general de la
ecuación de la vorticidad, como se hizo en la Sección
3.3.3 para obtener la ecuación (3.51).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
térmica.5.13
- Algunos autores denominan fluidos perfectos a
los fluidos no viscosos, y gases ideales a lo que aquí hemos
llamado gases perfectos.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Euler:5.14
- Prescindiremos en lo que sigue de las ecuaciones
de conservación de las especies.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fluidos.5.15
- Al no existir tampoco
fenómenos de difusión de masa en fluidos ideales, no sería
necesario precisar si los fluidos son miscibles o no.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... irrotacional,5.16
- Véanse
comentarios al final de esta sección.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
fluido.5.17
- Es decir, el flujo es homentrópico en todo
instante.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
potencial.5.18
- Las condiciones que se indican son sólo
suficientes. Una discusión más detallada y rigurosa puede
encontrarse en el texto de Liñán (1967).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pequeño:5.19
- Para poner esto de manifiesto,
sería necesario adimensionalizar la ecuación (5.76)
utilizando
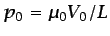 en la ecuación (4.6),
debido a que la presión en flujos a bajos números de Reynolds no
es del orden de
en la ecuación (4.6),
debido a que la presión en flujos a bajos números de Reynolds no
es del orden de
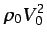 , sino de
, sino de
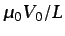 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...incomp-3).5.20
- El
rotacional de un gradiente es nulo y el orden de los operadores
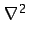 y
y
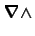 puede intercambiarse.
puede intercambiarse.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... demostrar5.21
- Véase, por ejemplo, Crespo (1997).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... superior,5.22
- La limitación en el
valor del número de Reynolds máximo vendrá dada por la necesaria
condición de que el flujo sea laminar.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....5.23
- Puede encontrarse una descripción más detallada de
este tipo de flujos en los textos de Crespo (1997) y
Batchelor (1967). Obsérvese que, si
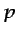 sólo depende de
sólo depende de 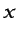 , de
la ecuación (5.81) se deduce que
, de
la ecuación (5.81) se deduce que 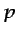 varía linealmente con
varía linealmente con
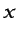 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... convectivo.5.24
- Puede consultarse,
por ejemplo, el texto de Batchelor (1967).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...dominante,5.25
- Una justificación más
detallada para despreciar los términos de difusión en las
ecuaciones de conservación de la cantidad de movimiento y de la
energía en el flujo considerado y en otros tipos de flujos puede
encontrarse en los textos de Crespo (1997) y Batchelor (1967),
por ejemplo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... grande5.26
- Obsérvese que un valor
muy pequeño de
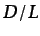 puede hacer que no se cumpla la condición de
la ecuación (5.90).
puede hacer que no se cumpla la condición de
la ecuación (5.90).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ejemplo5.27
- Peculiar en
el sentido de que el flujo de Hagen-Poiseuille en conductos de
sección circular es estable frente a perturbaciones
infinitesimales a cualquier número de Reynolds, lo que no
ocurre, por ejemplo, en el caso bidimensional.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...interna3-inc-2):5.28
- Obsérvese que, en realidad,
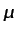 y
y
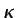 , pueden extraerse fuera del operador
, pueden extraerse fuera del operador
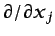 , al haberse supuesto constantes. Con respecto a la ecuación
(5.44), aparte de las simplificaciones ya
introducidas en ella, no tendremos en cuenta el último término
debido a radiación térmica y reacciones químicas.
, al haberse supuesto constantes. Con respecto a la ecuación
(5.44), aparte de las simplificaciones ya
introducidas en ella, no tendremos en cuenta el último término
debido a radiación térmica y reacciones químicas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
obtiene5.29
- Consúltese, por ejemplo, Crespo (1997).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
respectivamente).5.30
- Esto no está en contradicción con el
hecho de que los fenómenos de difusión por transporte molecular
son obviamente los únicos que realmente producen mezcla a nivel
molecular y uniformizan las distribuciones de las magnitudes
fluidas. Lo que ocurre en flujos turbulentos es que el movimiento
del fluido tiende a favorecer que dichos fenómenos de transporte
molecular se intensifiquen. Aunque no hemos hecho referencia en lo
anterior a procesos de difusión de masa de distintas especies (la
ecuación promediada que se obtendría a partir de la ecuación de
conservación de especies sería análoga a la ecuación (5.98)),
considérese un recipiente que contiene dos líquidos miscibles,
inicialmente separados, por ejemplo, por una superficie de
separación horizontal. Si no existe movimiento, la mezcla de los
líquidos puede requerir mucho tiempo. Si se agita durante unos
instantes, se puede conseguir un gran aumento del área de la
superficie a través de la cual se produce la difusión de ambos
líquidos, y reducir extraordinariamente el tiempo de mezcla.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
fluidas,5.31
- Debido a que no requieren ecuaciones
diferenciales en derivadas parciales adicionales, a este tipo de
modelos se les denomina en ocasiones modelos de ``cero
ecuaciones'').
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...:5.32
- El signo negativo permite expresar que el
flujo turbulento tenga el sentido adecuado con respecto al de
variación de
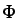 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
turbulenta,5.33
-
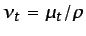 , siendo
, siendo 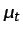 la
viscosidad turbulenta. En ocasiones se denomina viscosidad
efectiva a la suma de
la
viscosidad turbulenta. En ocasiones se denomina viscosidad
efectiva a la suma de 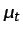 y la viscosidad del fluido
y la viscosidad del fluido 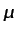 ,
siendo esta última mucho menor que
,
siendo esta última mucho menor que 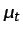 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... demostrar5.34
- Véase, por ejemplo, Crespo (1997).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
homentrópico5.35
- Según se ha indicado anteriormente, teniendo
en cuenta que el fluido es ideal, basta con que no exista adición
de calor por radiación y reacciones químicas y que todas las
líneas de corriente procedan de una región del flujo en la que la
entropía es uniforme, para que
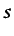 sea uniforme en todo el campo
fluido.
sea uniforme en todo el campo
fluido.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
remanso.5.36
- En puntos en los que la velocidad del fluido es
nula, las magnitudes termodinámicas coinciden con las de remanso.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...comp-i-4),5.37
- Una vez calculada la
distribución de
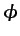 , la ecuación (5.129) permite determinar la
distribución de
, la ecuación (5.129) permite determinar la
distribución de 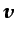 . A partir de la ecuación (5.136), conocida
la velocidad del sonido de remanso, puede entonces determinarse la
distribución de
. A partir de la ecuación (5.136), conocida
la velocidad del sonido de remanso, puede entonces determinarse la
distribución de 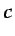 . Obsérvese que en este tipo de flujos, si se
conocen dos magnitudes de remanso y una magnitud termodinámica
(distinta de la entropía) o el módulo de la velocidad, es posible
determinar las restantes magnitudes y, en su caso, el módulo de la
velocidad.
. Obsérvese que en este tipo de flujos, si se
conocen dos magnitudes de remanso y una magnitud termodinámica
(distinta de la entropía) o el módulo de la velocidad, es posible
determinar las restantes magnitudes y, en su caso, el módulo de la
velocidad.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... incidente,5.38
- Véase, por ejemplo, Fletcher (1991).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lineal5.39
- En la ecuación (5.138),
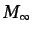 es el número de Mach del flujo incidente, que tiene la
dirección del eje
es el número de Mach del flujo incidente, que tiene la
dirección del eje 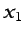 , y
, y 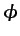 es el potencial de perturbación
que se superpone al correspondiente al flujo incidente.
es el potencial de perturbación
que se superpone al correspondiente al flujo incidente.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
choque.5.40
- Véase, por ejemplo, Crespo (1997).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... perfecto:5.41
- Los
subíndices 1 y 2 denotan valores aguas arriba y aguas abajo,
respectivamente, de la onda de choque;
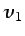 y
y 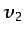 son
componentes de la velocidad normales a la onda.
son
componentes de la velocidad normales a la onda.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
natural5.42
- Flujos como el del Ejemplo 2 de la página
![[*]](crossref.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... temperatura,5.43
- Compruébese que se está
haciendo
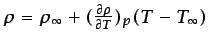 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
primitivas,6.1
- En una formulación que utiliza variables
primitivas, entre las variables dependientes aparecen la velocidad
y la presión, no la vorticidad y la función de corriente
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
primitivas,6.2
- Formulación que utiliza como variables
dependientes la velocidad y la presión (no la vorticidad y la
función de corriente).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.