En la Sección 1.1.1 se dijo que las tensiones cortantes en
el seno de un fluido dan lugar a deformaciones continuas, y que
las leyes constitutivas de los fluidos permiten precisamente
definir, análogamente a como se define en sólidos la relación
entre tensiones y deformaciones, la relación entre tensiones
cortantes y velocidades de deformación. Por otra parte, en la
Sección 1.5.4 se indicó que, debido al carácter vectorial
de la cantidad de movimiento, la relación entre el tensor de
tensiones
![]() y las derivadas
de las componentes del vector velocidad requería la discusión
previa de algunas propiedades cinemáticas del campo fluido, que
no fueron necesarias para introducir las leyes de Fourier y de
Fick, ni la ley de Newton de la viscosidad en un flujo con
cortadura simple como el esquematizado en la Figura
1.1. Se trata de analizar en esta sección cómo es el
movimiento de un fluido en el entorno de un punto, con objeto de
describir la deformación que experimenta un elemento de fluido en
el tiempo.
y las derivadas
de las componentes del vector velocidad requería la discusión
previa de algunas propiedades cinemáticas del campo fluido, que
no fueron necesarias para introducir las leyes de Fourier y de
Fick, ni la ley de Newton de la viscosidad en un flujo con
cortadura simple como el esquematizado en la Figura
1.1. Se trata de analizar en esta sección cómo es el
movimiento de un fluido en el entorno de un punto, con objeto de
describir la deformación que experimenta un elemento de fluido en
el tiempo.
Consideremos, en un mismo instante ![]() , dos puntos en el campo
fluido separados una distancia
d
, dos puntos en el campo
fluido separados una distancia
d![]() : el punto de
referencia
: el punto de
referencia ![]() y
y
![]() d
d![]() . La
diferencia de velocidad entre ellos vendrá dada por
. La
diferencia de velocidad entre ellos vendrá dada por
Es fácil demostrar2.8que el tensor antisimétrico
![]() da lugar a una velocidad relativa
da lugar a una velocidad relativa
Puede también demostrarse2.9 que cada una de las componentes de la diagonal
principal del tensor de velocidades de deformación (![]() )
representa el ritmo de deformación longitudinal de un elemento de
línea fluida paralelo a la dirección del eje de coordenadas
correspondiente a
)
representa el ritmo de deformación longitudinal de un elemento de
línea fluida paralelo a la dirección del eje de coordenadas
correspondiente a ![]() , relativo a la longitud del elemento (o
velocidad de dilatación lineal unitaria); por ejemplo,
, relativo a la longitud del elemento (o
velocidad de dilatación lineal unitaria); por ejemplo,
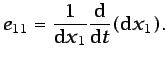 |
(2.20) |
Es también muy interesante comprobar que
A las contribuciones al movimiento en el entorno de un punto que
se acaban de describir, asociadas a la rotación del elemento
fluido como un sólido rígido y a su deformación, debe añadirse la
debida a la traslación uniforme del elemento con la velocidad
local del fluido
![]() .
.