



Next: Flujos bidimensionales. Concepto de
Up: Aproximaciones de tipo cinemático
Previous: Flujos con distribución de
Índice General
Flujos irrotacionales. Concepto de potencial de
velocidad
Como se ha indicado anteriormente, en este tipo de flujos se
satisface la condición
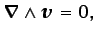 |
(5.6) |
de forma que la distribución de las tres componentes de la
velocidad queda determinada a partir de una única función escalar
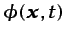 , denominada potencial de velocidad:
, denominada potencial de velocidad:
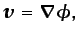 |
(5.7) |
razón por la cual a los flujos irrotacionales se les denomina
también flujos potenciales.
La ecuación de conservación de la masa puede entonces expresarse
de la forma
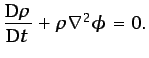 |
(5.8) |
Cuando
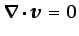 (flujo
incompresible),
(flujo
incompresible), 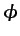 es una función potencial que satisface
es una función potencial que satisface
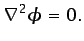 |
(5.9) |
La ecuación (3.36) de conservación de la cantidad de
movimiento, teniendo en cuenta la ecuación (3.40), se simplifica y
queda como sigue:5.2
![$\displaystyle \rho\vec{\nabla}\left[\frac{\partial \phi}{\partial t} + \frac{1}...
...t] =-\vec{\nabla}p + (\lambda + 2\mu)\vec{\nabla}(\nabla^2\phi)+ \rho\vec{f}_m.$](img527.gif) |
(5.10) |
Si las fuerzas másicas derivan de un potencial 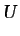 , y puede
suponerse que
, y puede
suponerse que 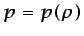 , es decir, que existe una relación de
barotropía que permite expresar
, es decir, que existe una relación de
barotropía que permite expresar
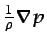 como
el gradiente de una función escalar
como
el gradiente de una función escalar
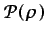 (tal como
se discutirá en la Sección 5.3.1), al integrar la ecuación anterior
se obtiene
(tal como
se discutirá en la Sección 5.3.1), al integrar la ecuación anterior
se obtiene
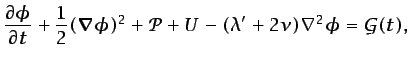 |
(5.11) |
siendo
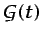 una función de
una función de 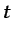 y
y
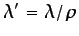 . Si la densidad del fluido es constante
(con lo que
. Si la densidad del fluido es constante
(con lo que
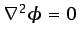 , de acuerdo con la ecuación
(5.9), y
, de acuerdo con la ecuación
(5.9), y
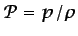 ), resulta
), resulta
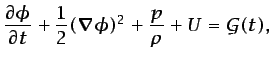 |
(5.12) |
y si además el flujo es estacionario (el primer término de la
ecuación (5.11) es nulo y obviamente
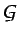 no depende de
no depende de 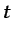 ), se obtiene finalmente la
denominada ecuación de Bernoulli para flujos
irrotacionales,
), se obtiene finalmente la
denominada ecuación de Bernoulli para flujos
irrotacionales,
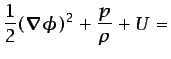 constante constante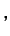 |
(5.13) |
o bien,
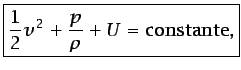 |
(5.14) |
siendo
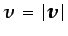 (no debe confundirse con la componente
cartesiana del vector
(no debe confundirse con la componente
cartesiana del vector 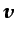 según el eje
según el eje 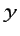 que aparece en otros contextos).
que aparece en otros contextos).
Obsérvese que en la discusión anterior no hemos supuesto en ningún
momento que el fluido sea ideal (es decir, con viscosidad nula),
lo que quizá esté en aparente contradicción con la noción previa
que el lector pueda tener de que la ecuación de Bernoulli es
aplicable cuando los efectos de la viscosidad son despreciables.
Esto se debe a que se ha supuesto que el flujo es incompresible,
en cuyo caso se satisface5.3 que
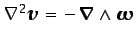 , lo que determina que
, lo que determina que
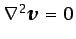 cuando el flujo es irrotacional y, por tanto,
que el término de difusión de cantidad de movimiento se anule, lo
cual obviamente ocurriría también cuando la viscosidad del fluido
fuese nula.5.4
cuando el flujo es irrotacional y, por tanto,
que el término de difusión de cantidad de movimiento se anule, lo
cual obviamente ocurriría también cuando la viscosidad del fluido
fuese nula.5.4




Next: Flujos bidimensionales. Concepto de
Up: Aproximaciones de tipo cinemático
Previous: Flujos con distribución de
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![]() , lo que determina que
, lo que determina que
![]() cuando el flujo es irrotacional y, por tanto,
que el término de difusión de cantidad de movimiento se anule, lo
cual obviamente ocurriría también cuando la viscosidad del fluido
fuese nula.5.4
cuando el flujo es irrotacional y, por tanto,
que el término de difusión de cantidad de movimiento se anule, lo
cual obviamente ocurriría también cuando la viscosidad del fluido
fuese nula.5.4