



Next: Ecuación de conservación de
Up: Ecuación de conservación de
Previous: Ecuaciones de Navier-Stokes
Índice General
Ecuación de la vorticidad
La ecuación de conservación de la cantidad de movimiento puede
expresarse de otra forma alternativa más introduciendo la
identidad3.12
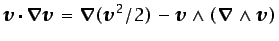 |
(3.40) |
y
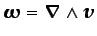 en el primer término de
la ecuación (3.23). Dividiendo por
en el primer término de
la ecuación (3.23). Dividiendo por 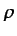 la expresión
resultante, se obtiene
la expresión
resultante, se obtiene
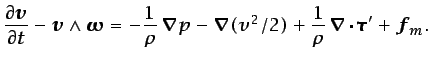 |
(3.41) |
Tomando el rotacional de la ecuación anterior se obtiene la
ecuación de Helmholtz:
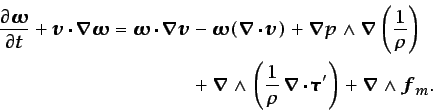 |
(3.42) |
Si el flujo es incompresible
(
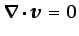 ) y la viscosidad cinemática
uniforme, teniendo en cuenta la ley de Navier-Poisson de la
ecuación (3.27), el penúltimo término de la ecuación
(3.42) queda de la forma siguiente:
) y la viscosidad cinemática
uniforme, teniendo en cuenta la ley de Navier-Poisson de la
ecuación (3.27), el penúltimo término de la ecuación
(3.42) queda de la forma siguiente:
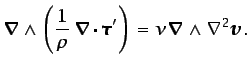 |
(3.43) |
La condición
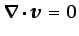 también permite
simplificar la identidad vectorial de la ecuación
(3.34), obteniéndose
también permite
simplificar la identidad vectorial de la ecuación
(3.34), obteniéndose
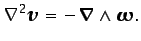 |
(3.44) |
Introduciendo este resultado en la ecuación (3.43), y ésta
a su vez en la ecuación (3.42), y utilizando las
condiciones de que el fluido sea de densidad uniforme y de que
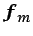 derive de una función potencial, la ecuación
(3.42) queda de la forma siguiente:
derive de una función potencial, la ecuación
(3.42) queda de la forma siguiente:
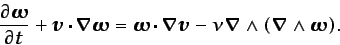 |
(3.45) |
La ecuación (3.34) aplicada al vector
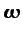 ,
,
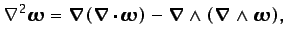 |
(3.46) |
teniendo en cuenta que
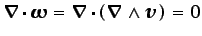 |
(3.47) |
al ser el operador vectorial
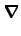 ortogonal a
ortogonal a
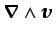 , se reduce a
, se reduce a
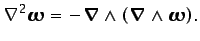 |
(3.48) |
Sustituyendo esta última ecuación en el último término de la
ecuación (3.45), ésta queda finalmente de la forma
siguiente:3.13
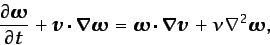 |
(3.49) |
o bien,
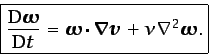 |
(3.50) |
Obsérvese que, dado que
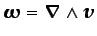 ,
la única variable dependiente en la ecuación (3.49) es
,
la única variable dependiente en la ecuación (3.49) es
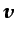 , no apareciendo en ella el término correspondiente al
término de presión que aparecía en la ecuación (3.42).
, no apareciendo en ella el término correspondiente al
término de presión que aparecía en la ecuación (3.42).
Es obvio que en un flujo bidimensional
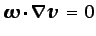 , con lo que la
ecuación (3.50) se reduce a
, con lo que la
ecuación (3.50) se reduce a
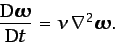 |
(3.51) |
En el flujo de un fluido sin viscosidad (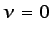 ),
),
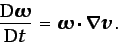 |
(3.52) |




Next: Ecuación de conservación de
Up: Ecuación de conservación de
Previous: Ecuaciones de Navier-Stokes
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![]() ) y la viscosidad cinemática
uniforme, teniendo en cuenta la ley de Navier-Poisson de la
ecuación (3.27), el penúltimo término de la ecuación
(3.42) queda de la forma siguiente:
) y la viscosidad cinemática
uniforme, teniendo en cuenta la ley de Navier-Poisson de la
ecuación (3.27), el penúltimo término de la ecuación
(3.42) queda de la forma siguiente:
![]() ,
la única variable dependiente en la ecuación (3.49) es
,
la única variable dependiente en la ecuación (3.49) es
![]() , no apareciendo en ella el término correspondiente al
término de presión que aparecía en la ecuación (3.42).
, no apareciendo en ella el término correspondiente al
término de presión que aparecía en la ecuación (3.42).
![]() , con lo que la
ecuación (3.50) se reduce a
, con lo que la
ecuación (3.50) se reduce a
![]() ),
),