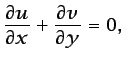 |
(5.45) |
En flujos bidimensionales y laminares de fluidos que se comportan como incompresibles es posible considerar una formulación alternativa a la correspondiente a las ecuaciones (5.38) y (5.39), que en este caso toman la forma
Tomando la derivada parcial con respecto a ![]() en la ecuación
(5.46) y la derivada parcial con respecto a
en la ecuación
(5.46) y la derivada parcial con respecto a ![]() en la
ecuación (5.47), y restando las igualdades resultantes, se
obtiene
en la
ecuación (5.47), y restando las igualdades resultantes, se
obtiene
Por otra parte, introduciendo la función de corriente definida en las ecuaciones (5.16) y (5.17),
Esta formulación vorticidad/función de corriente queda por tanto definida mediante las ecuaciones (5.48), (5.50) y (5.51). La sustitución de las expresiones de la ecuación (5.50) en la ecuación (5.48) eliminaría la presencia explícita de las componentes de la velocidad, resultando un sistema formado por las ecuaciones
Una vez resueltas las ecuaciones (5.52) y (5.53), es posible obtener la distribución de presión reducida resolviendo la siguiente ecuación
En problemas tridimensionales es también posible, en principio, utilizar una formulación de este tipo, aunque en este caso la vorticidad tiene tres componentes y la función de corriente debe sustituirse por un potencial vector.