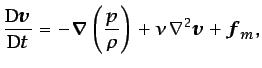Next: Formulación basada en la
Up: Simplificaciones de las leyes
Previous: Gases perfectos
Índice General
En flujos de fluidos incompresibles la distribución de velocidad
es solenoidal (
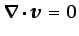 ), por lo que son
aplicables los comentarios realizados en la Sección 5.2.1.
), por lo que son
aplicables los comentarios realizados en la Sección 5.2.1.
En realidad, esta sección podría haberse incluido en la Sección
5.4, ya que la justificación5.10 de la aproximación que supone despreciar los efectos de
compresibilidad no es trivial, y requiere analizar con detalle las
ecuaciones del movimiento. En el texto de Batchelor (1967) (p. 167 y siguientes) se examinan las condiciones bajo las cuales es
aceptable la simplificación que supone considerar el fluido como
incompresible. En esta sección nos limitaremos a aceptar que es
posible aplicar la condición de que
D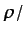 D
D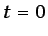 .
.
Es importante destacar que en flujos de fluidos incompresibles la
presión es una variable dependiente que no puede expresarse, como
ocurre en el caso de flujos compresibles, en función de otras
variables de estado. Como ya se indicó en la sección de
introducción de este capítulo y en el Capítulo 4, si la
viscosidad no depende de la temperatura las ecuaciones de
conservación de la masa, que con la condición
D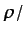 D
D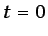 se reduce a
se reduce a
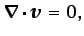 |
(5.38) |
y de cantidad de movimiento,
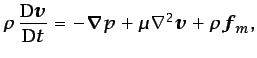 |
(5.39) |
quedan desacopladas de la ecuación de conservación de la energía,
y pueden ser resueltas independientemente de ésta. Las variables
dependientes que intervienen en el problema mecánico son
exclusivamente las tres componentes de la velocidad y la presión.
Dado que la presión sólo interviene en la ecuación
(5.39), obsérvese que es posible restar una constante a
la presión en dicha ecuación sin que ello afecte a la solución:
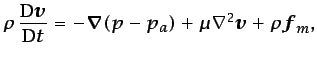 |
(5.40) |
Cuando 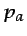 es la presión atmosférica, a la variable
es la presión atmosférica, a la variable 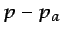 se
la denomina presión manométrica. Es frecuente en este tipo
de flujos resolver las ecuaciones utilizando la presión
manométrica como variable dependiente.
se
la denomina presión manométrica. Es frecuente en este tipo
de flujos resolver las ecuaciones utilizando la presión
manométrica como variable dependiente.
Si el fluido, además de incompresible, es de densidad uniforme, la
ecuación (5.39) puede ponerse de la forma
siguiente:
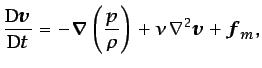 |
(5.41) |
y si las fuerzas másicas derivan de un potencial 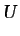 ,
,
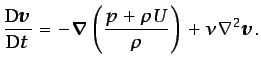 |
(5.42) |
Obsérvese que puede definirse una nueva variable,
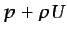 ,
denominada habitualmente presión reducida, para la que se
obtendría una solución idéntica a la que se hallaría para
,
denominada habitualmente presión reducida, para la que se
obtendría una solución idéntica a la que se hallaría para 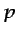 en
ausencia de fuerzas másicas. Una vez determinada la distribución
de presión reducida, y conocido el potencial de fuerzas másicas,
es posible determinar la distribución de presión.
en
ausencia de fuerzas másicas. Una vez determinada la distribución
de presión reducida, y conocido el potencial de fuerzas másicas,
es posible determinar la distribución de presión.
La ecuación (3.64) de conservación de la energía queda
de la forma
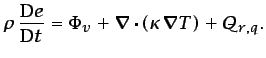 |
(5.43) |
Esta ecuación, utilizando como dato para su resolución la
distribución de velocidad determinada a partir exclusivamente de
las ecuaciones mecánicas, permite obtener la distribución de
temperatura en el fluido. Es muy frecuente que el término 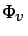 de disipación viscosa sea muy pequeño en flujos de fluidos que se
comportan como incompresibles, salvo en algunos casos de líquidos
muy viscosos que se muevan a alta velocidad en conductos muy
pequeños, por lo que la ecuación (5.43) suele
simplificarse, quedando
de disipación viscosa sea muy pequeño en flujos de fluidos que se
comportan como incompresibles, salvo en algunos casos de líquidos
muy viscosos que se muevan a alta velocidad en conductos muy
pequeños, por lo que la ecuación (5.43) suele
simplificarse, quedando
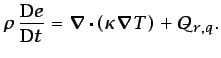 |
(5.44) |
Subsecciones




Next: Formulación basada en la
Up: Simplificaciones de las leyes
Previous: Gases perfectos
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![]() ), por lo que son
aplicables los comentarios realizados en la Sección 5.2.1.
), por lo que son
aplicables los comentarios realizados en la Sección 5.2.1.
![]() D
D![]() .
.
![]() D
D![]() se reduce a
se reduce a