



Next: Ecuación de conservación de
Up: Ecuaciones generales de la
Previous: Ecuaciones generales de la
Índice General
En este capítulo se utilizará frecuentemente el concepto
de volumen fluido (o sistema material). Un volumen fluido
es cualquier porción de fluido separada del resto por una
superficie fluida3.1 cerrada, y por tanto está
constituido en todo momento por las mismas partículas
fluidas.3.2 Un volumen fluido es, por tanto, un volumen
material, de forma análoga a como una superficie fluida es una
superficie material. Durante el movimiento, el volumen fluido
cambia de forma y va ocupando diferentes regiones
del espacio. En sucesivos instantes, el volumen de la región
ocupada por el volumen fluido se denotará con 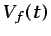 . La masa
del volumen fluido, que obviamente permanecerá constante en el
tiempo, es
. La masa
del volumen fluido, que obviamente permanecerá constante en el
tiempo, es
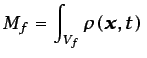 d d |
(3.1) |
Análogamente, si
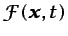 es una función continua
que define en cada punto e instante una magnitud cualquiera por unidad
de volumen (p. ej., la energía interna por unidad de volumen,
es una función continua
que define en cada punto e instante una magnitud cualquiera por unidad
de volumen (p. ej., la energía interna por unidad de volumen,
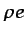 , o la cantidad de movimiento por unidad de volumen,
, o la cantidad de movimiento por unidad de volumen,
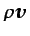 ), la correspondiente magnitud3.3 asociada
al volumen fluido
), la correspondiente magnitud3.3 asociada
al volumen fluido 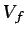 es
es
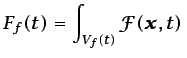 d d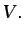 |
(3.2) |
En las secciones siguientes, en las que se introducirán las
ecuaciones que expresan los principios de conservación que
describen el movimiento de los fluidos, será necesario hacer uso
de la derivada material
d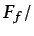 d
d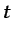 . Dado que la
integral de la ecuación (3.2) está extendida a un volumen
variable en el tiempo,
. Dado que la
integral de la ecuación (3.2) está extendida a un volumen
variable en el tiempo, 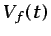 , no es posible introducir el
operador derivada dentro de la integral y aplicarlo sólo al
integrando. Si
, no es posible introducir el
operador derivada dentro de la integral y aplicarlo sólo al
integrando. Si 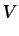 es el volumen geométrico fijo (volumen de
control) que ocupa el volumen fluido en el instante en el que se
expresa la derivada, es fácil deducir,3.4mediante consideraciones puramente cinemáticas,
es el volumen geométrico fijo (volumen de
control) que ocupa el volumen fluido en el instante en el que se
expresa la derivada, es fácil deducir,3.4mediante consideraciones puramente cinemáticas,
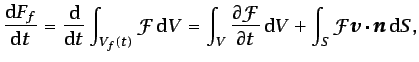 |
(3.3) |
siendo 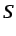 la superficie cerrada que limita
la superficie cerrada que limita 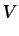 . La ecuación
(3.3) expresa el denominado teorema del transporte de
Reynolds, y los dos términos del último miembro pueden
interpretarse fácilmente: el primero representa la variación en el
tiempo que experimenta la magnitud
. La ecuación
(3.3) expresa el denominado teorema del transporte de
Reynolds, y los dos términos del último miembro pueden
interpretarse fácilmente: el primero representa la variación en el
tiempo que experimenta la magnitud 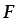 en el volumen fijo
en el volumen fijo 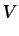 , y
el segundo, el flujo neto saliente de
, y
el segundo, el flujo neto saliente de 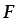 a través de la
superficie fija
a través de la
superficie fija 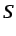 .
.




Next: Ecuación de conservación de
Up: Ecuaciones generales de la
Previous: Ecuaciones generales de la
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
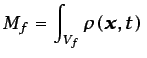 d
d