



Next: Leyes constitutivas de fluidos
Up: Forma diferencial
Previous: Forma diferencial
Índice General
Ley de Navier-Poisson
En la Sección 1.5.4 se introdujo la ley de la ecuación
(1.44) para el flujo con cortadura simple de la Figura
1.1, y se comentó que la relación entre el tensor
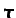 y las derivadas del vector velocidad, análoga a las
establecidas por las leyes de Fourier y Fick (con la salvedad de
que en este caso la magnitud que se transporta es vectorial), se
introduciría después de discutir algunos conceptos cinemáticos.
Esto es lo que se va a hacer a continuación, una vez analizado el
movimiento relativo en el entorno de un punto en la Sección
2.4.
y las derivadas del vector velocidad, análoga a las
establecidas por las leyes de Fourier y Fick (con la salvedad de
que en este caso la magnitud que se transporta es vectorial), se
introduciría después de discutir algunos conceptos cinemáticos.
Esto es lo que se va a hacer a continuación, una vez analizado el
movimiento relativo en el entorno de un punto en la Sección
2.4.
En la Sección 1.3.2 se introdujo la siguiente
descomposición del tensor de tensiones:
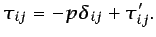 |
(3.25) |
Si el fluido está en reposo, las componentes del tensor de
tensiones debidas a la viscosidad,
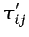 , son nulas, y el estado tensional queda definido por
la presión. Las tensiones
, son nulas, y el estado tensional queda definido por
la presión. Las tensiones
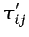 que aparecen en fluidos
en movimiento están asociadas a la desviación respecto del estado
de equilibrio debida a dicho movimiento. La ley experimental de
Navier-Poisson, aplicable a fluidos newtonianos, relaciona las
tensiones debidas a la viscosidad
que aparecen en fluidos
en movimiento están asociadas a la desviación respecto del estado
de equilibrio debida a dicho movimiento. La ley experimental de
Navier-Poisson, aplicable a fluidos newtonianos, relaciona las
tensiones debidas a la viscosidad
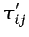 con las
componentes
con las
componentes 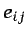 del tensor de velocidades de deformación
definido en la ecuación (2.17), estableciendo una
proporcionalidad entre ellas:
del tensor de velocidades de deformación
definido en la ecuación (2.17), estableciendo una
proporcionalidad entre ellas:
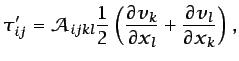 |
(3.26) |
siendo
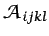 un tensor de cuarto orden (81 términos).
Dado que los fluidos newtonianos son isótropos, la ecuación
(3.26) en realidad se simplifica y queda de la forma
un tensor de cuarto orden (81 términos).
Dado que los fluidos newtonianos son isótropos, la ecuación
(3.26) en realidad se simplifica y queda de la forma
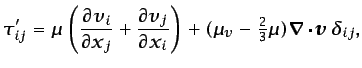 |
(3.27) |
siendo 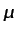 el coeficiente de viscosidad (viscosidad dinámica) ya
introducido en la Sección 1.5.4, y
el coeficiente de viscosidad (viscosidad dinámica) ya
introducido en la Sección 1.5.4, y 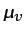 un segundo
coeficiente de viscosidad que sólo es relevante en problemas muy
particulares. Obsérvese que el último término de esta ecuación se
anula cuando el fluido se comporta como incompresible (al ser en
este caso
un segundo
coeficiente de viscosidad que sólo es relevante en problemas muy
particulares. Obsérvese que el último término de esta ecuación se
anula cuando el fluido se comporta como incompresible (al ser en
este caso
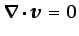 ), y que la suma de los
elementos de la diagonal principal del tensor de
tensiones debidas a la viscosidad es
), y que la suma de los
elementos de la diagonal principal del tensor de
tensiones debidas a la viscosidad es
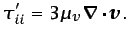 |
(3.28) |
Es posible definir la ``presión mecánica'' en un punto como la
media (con signo opuesto) de las tres tensiones de la diagonal
principal del tensor de tensiones en
dicho punto:
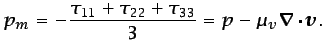 |
(3.29) |
Obsérvese que la ecuación anterior establece una relación entre la
presión mecánica y la presión termodinámica, que coinciden si el
flujo es incompresible (
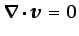 ) o el fluido
es un gas monoatómico (
) o el fluido
es un gas monoatómico (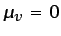 ).3.9 El efecto de
).3.9 El efecto de 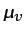 puede ser
importante en el estudio de la estructura de ondas de choque, por
ejemplo, pero en general suele ser despreciable incluso para gases
poliatómicos, y puede suponerse también para éstos
puede ser
importante en el estudio de la estructura de ondas de choque, por
ejemplo, pero en general suele ser despreciable incluso para gases
poliatómicos, y puede suponerse también para éstos 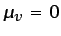 .
.




Next: Leyes constitutivas de fluidos
Up: Forma diferencial
Previous: Forma diferencial
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![]() y las derivadas del vector velocidad, análoga a las
establecidas por las leyes de Fourier y Fick (con la salvedad de
que en este caso la magnitud que se transporta es vectorial), se
introduciría después de discutir algunos conceptos cinemáticos.
Esto es lo que se va a hacer a continuación, una vez analizado el
movimiento relativo en el entorno de un punto en la Sección
2.4.
y las derivadas del vector velocidad, análoga a las
establecidas por las leyes de Fourier y Fick (con la salvedad de
que en este caso la magnitud que se transporta es vectorial), se
introduciría después de discutir algunos conceptos cinemáticos.
Esto es lo que se va a hacer a continuación, una vez analizado el
movimiento relativo en el entorno de un punto en la Sección
2.4.