



Next: Otros tipos de flujos
Up: Aproximaciones de tipo cinemático
Previous: Flujos irrotacionales. Concepto de
Índice General
Flujos bidimensionales. Concepto de función de
corriente
Como ya se indicó en la Sección 2.3, un flujo
bidimensional es un flujo plano (una de las componentes del vector
velocidad en un sistema de referencia cartesiano es nula) en el
que el vector velocidad no varía en dirección perpendicular al
plano que lo contiene:
En estos flujos, cuando el fluido es incompresible, la ecuación
(3.11), que en este caso se reduce a
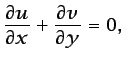 |
(5.15) |
garantiza la existencia de una función
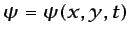 ,
denominada función de corriente, definida
por5.5
,
denominada función de corriente, definida
por5.5
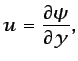 |
(5.16) |
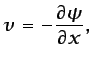 |
(5.17) |
de forma que
Obsérvese que el campo de velocidades queda completamente definido
una vez conocida la función
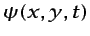 . Ésta puede determinarse
en cualquier punto
. Ésta puede determinarse
en cualquier punto 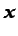 , salvo por una constante de
integración, mediante
, salvo por una constante de
integración, mediante
donde la integral curvilínea puede hacerse a través de cualquier
línea de integración que una 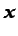 con el punto
con el punto 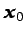 ,
en el que
,
en el que
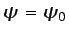 .
.
Asimismo obsérvese que las líneas de corriente definidas en la
ecuación (2.14) son líneas en las que
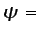 constante. Por tanto, las líneas de
constante. Por tanto, las líneas de
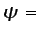 constante son tangentes al vector velocidad en cada
punto, de lo que se deduce que el flujo volumétrico a través de
ellas debe ser nulo. Teniendo esto último en cuenta, aplicando la
ecuación (3.5) al volumen ``bidimensional'' sombreado de
la Figura 5.1,
constante son tangentes al vector velocidad en cada
punto, de lo que se deduce que el flujo volumétrico a través de
ellas debe ser nulo. Teniendo esto último en cuenta, aplicando la
ecuación (3.5) al volumen ``bidimensional'' sombreado de
la Figura 5.1,
se deduce que el flujo volumétrico por unidad de
longitud5.6
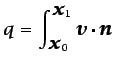
d
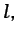
es el mismo, e igual a
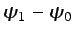 , a través de cualquier
línea que una dos puntos cualesquiera
, a través de cualquier
línea que una dos puntos cualesquiera 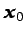 y
y 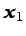 ,
situados en sendas líneas de corriente definidas por
,
situados en sendas líneas de corriente definidas por 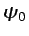 y
y
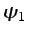 , respectivamente. Si en un flujo se representan las
líneas de corriente correspondientes a valores equiespaciados de
, respectivamente. Si en un flujo se representan las
líneas de corriente correspondientes a valores equiespaciados de
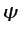 , la distancia entre ellas será inversamente proporcional a
la velocidad del fluido.
, la distancia entre ellas será inversamente proporcional a
la velocidad del fluido.
En un flujo plano, la vorticidad tiene una única componente en
dirección perpendicular al plano que contiene a 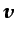 :
:
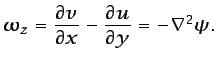 |
(5.19) |
Si el flujo es, además de incompresible, irrotacional, se tiene,
en vista de la ecuación anterior,
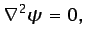 |
(5.20) |
y, teniendo en cuenta la ecuación (5.7),
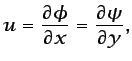 |
(5.21) |
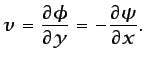 |
(5.22) |
Las segundas igualdades de las ecuaciones (5.21) y
(5.22) expresan las condiciones de Cauchy-Riemann que
aparecen en la teoría de funciones de variable compleja. Estas
condiciones son necesarias y suficientes (si las derivadas en las
ecuaciones (5.21) y (5.22) son continuas) para que
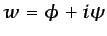 sea una función analítica de la variable
compleja
sea una función analítica de la variable
compleja
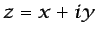 . A la función
. A la función 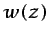 se le denomina
potencial complejo.5.7 En principio, por tanto,
cualquier función analítica de
se le denomina
potencial complejo.5.7 En principio, por tanto,
cualquier función analítica de 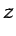 puede proporcionar un campo de
velocidades irrotacional en un flujo incompresible.
puede proporcionar un campo de
velocidades irrotacional en un flujo incompresible.
Las componentes de 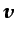 están directamente relacionadas con
d
están directamente relacionadas con
d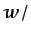 d
d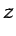 :
:
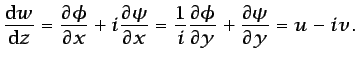 |
(5.23) |
Obsérvese que, dado que las líneas de
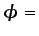 constante y
las líneas de corriente
constante y
las líneas de corriente
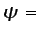 constante son
perpendiculares (
constante son
perpendiculares (
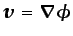 ) y tangentes,
respectivamente, al vector velocidad, ambos tipos de líneas deben
ser perpendiculares entre sí.
) y tangentes,
respectivamente, al vector velocidad, ambos tipos de líneas deben
ser perpendiculares entre sí.
Cuando el fluido es compresible pero el flujo es estacionario, de
forma que la ecuación de continuidad queda de la forma
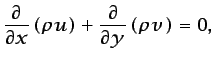 |
(5.24) |
puede introducirse también una función de corriente, aunque su
utilización no resultan tan interesante como en el caso de flujo
incompresible.




Next: Otros tipos de flujos
Up: Aproximaciones de tipo cinemático
Previous: Flujos irrotacionales. Concepto de
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![]() . Ésta puede determinarse
en cualquier punto
. Ésta puede determinarse
en cualquier punto ![]() , salvo por una constante de
integración, mediante
, salvo por una constante de
integración, mediante
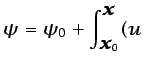 d
d![]() constante. Por tanto, las líneas de
constante. Por tanto, las líneas de
![]() constante son tangentes al vector velocidad en cada
punto, de lo que se deduce que el flujo volumétrico a través de
ellas debe ser nulo. Teniendo esto último en cuenta, aplicando la
ecuación (3.5) al volumen ``bidimensional'' sombreado de
la Figura 5.1,
constante son tangentes al vector velocidad en cada
punto, de lo que se deduce que el flujo volumétrico a través de
ellas debe ser nulo. Teniendo esto último en cuenta, aplicando la
ecuación (3.5) al volumen ``bidimensional'' sombreado de
la Figura 5.1,
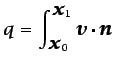 d
d![]() :
:
![]() están directamente relacionadas con
d
están directamente relacionadas con
d![]() d
d![]() :
:
![]() constante y
las líneas de corriente
constante y
las líneas de corriente
![]() constante son
perpendiculares (
constante son
perpendiculares (
![]() ) y tangentes,
respectivamente, al vector velocidad, ambos tipos de líneas deben
ser perpendiculares entre sí.
) y tangentes,
respectivamente, al vector velocidad, ambos tipos de líneas deben
ser perpendiculares entre sí.