



Next: Ley de Navier-Poisson
Up: Ecuación de conservación de
Previous: Forma integral
Índice General
Utilizando el teorema de Gauss para transformar las integrales de
superficie en integrales de volumen, la ecuación (3.17) puede
expresarse, en notación de subíndices, de la forma siguiente:
![$\displaystyle \int_{V}\left[\frac{\partial (\rho v_i)}{\partial t} + \frac{\par...
...artial x_j} - \frac{\partial \tau_{ij}}{\partial x_j} - \rho f_{m_{i}}\right] $](img285.gif) d d |
(3.18) |
Dado que cualquier volumen geométrico fijo es ocupado en cada
instante por un cierto volumen fluido, la ecuación (3.18) es
aplicable a cualquier volumen fijo 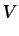 . Teniendo en cuenta esto y
la continuidad de las magnitudes fluidas y sus derivadas, se
deduce que el integrando de la ecuación (3.18) debe ser nulo:
. Teniendo en cuenta esto y
la continuidad de las magnitudes fluidas y sus derivadas, se
deduce que el integrando de la ecuación (3.18) debe ser nulo:
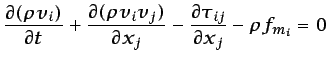 |
(3.19) |
(ecuación en forma conservativa). Teniendo en cuenta la ecuación
(3.8), que en notación de subíndices se expresa
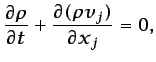 |
(3.20) |
la ecuación (3.19) puede escribirse de la siguiente forma
no conservativa:
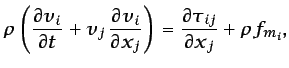 |
(3.21) |
o, en notación vectorial,
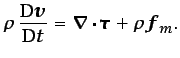 |
(3.22) |
La ecuación (3.22) expresa que la fuerza de inercia por
unidad de volumen (producto de la densidad por la aceleración) que
experimenta una partícula fluida es igual a la resultante de las
fuerzas de superficie y de volumen que actúan por unidad de
volumen sobre la partícula fluida. Introduciendo la ecuación
(1.9) en la ecuación (3.22), resulta
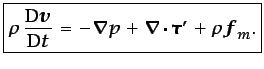 |
(3.23) |
La ecuación (3.23) puede expresarse en la forma
conservativa de la ecuación (3.19):
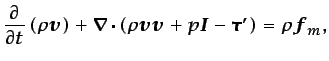 |
(3.24) |
donde 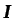 es el tensor identidad y
es el tensor identidad y
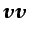 un
tensor de segundo orden.3.8
un
tensor de segundo orden.3.8
Subsecciones




Next: Ley de Navier-Poisson
Up: Ecuación de conservación de
Previous: Forma integral
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![$\displaystyle \int_{V}\left[\frac{\partial (\rho v_i)}{\partial t} + \frac{\par...
...artial x_j} - \frac{\partial \tau_{ij}}{\partial x_j} - \rho f_{m_{i}}\right] $](img285.gif) d
d