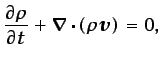 |
(4.1) |
Considérese un flujo de un gas perfecto4.1 descrito por las ecuaciones (3.8), (3.30) y (3.69) (introduciendo en esta última la ley de Fourier), con unas condiciones iniciales y de contorno determinadas:
Se van a definir las siguientes magnitudes adimensionales:
Si se divide cada una de las ecuaciones (4.8) a (4.10) por el factor que aparece en cada una de ellas en el término convectivo (segundo término), se obtiene
Las magnitudes entre llaves en las ecuaciones (4.11) a (4.14) son ahora adimensionales. Teniendo en cuenta las siguientes definiciones de números adimensionales:
Es importante entender las conclusiones e implicaciones del
análisis que se acaba de realizar. Ya se indicó que la solución de
la ecuaciones (4.1) a (4.4), determinada por las
distribuciones de ![]() ,
, ![]() ,
, ![]() ,
, ![]() y
y ![]() en función de
en función de ![]() ,
, ![]() ,
,
![]() y
y ![]() , dependerá de los parámetros que aparecen en dichas
ecuaciones y en las condiciones iniciales y de contorno. Los
parámetros que se han utilizado para adimensionalizar las
ecuaciones, junto con los restantes que aparecen en ellas, son los
siguientes:
, dependerá de los parámetros que aparecen en dichas
ecuaciones y en las condiciones iniciales y de contorno. Los
parámetros que se han utilizado para adimensionalizar las
ecuaciones, junto con los restantes que aparecen en ellas, son los
siguientes: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() y
y ![]() . Es inmediato observar tras una
simple inspección de las ecuaciones (4.21) a
(4.24) que la solución dada por las variables
adimensionales
. Es inmediato observar tras una
simple inspección de las ecuaciones (4.21) a
(4.24) que la solución dada por las variables
adimensionales ![]() ,
, ![]() ,
, ![]() ,
, ![]() y
y ![]() en función de
en función de
![]() ,
, ![]() ,
, ![]() y
y ![]() sólo dependerá de los seis números
adimensionales siguientes: St, Re, Pr, Fr, M y
sólo dependerá de los seis números
adimensionales siguientes: St, Re, Pr, Fr, M y ![]() , y de
aquellos que pudiesen aparecer en las condiciones iniciales y de
contorno adimensionalizadas. Esto significa que la dependencia de
la solución con respecto a los parámetros que intervienen en el
problema ha podido ser simplificada de forma notable, y que, una
vez obtenida la solución en forma adimensional para un conjunto
determinado de valores de los parámetros que intervienen, dicha
solución permitirá determinar la solución correspondiente a
cualquier otro conjunto de valores de parámetros siempre que éstos
proporcionen los mismos valores de los números adimensionales que
aquellos para los que fue obtenida la solución adimensional. Éste
es un resultado extraordinariamente útil también en mecánica de
fluidos experimental: la descripción de un flujo puede hacerse a
partir de los resultados de un experimento en el que las
condiciones sean semejantes a las que existen en dicho flujo. La
semejanza entre dos flujos queda precisamente garantizada por la
igualdad de los números adimensionales relevantes en el problema,
determinados a partir de los parámetros que definen las
condiciones que describen cada uno de los flujos.
, y de
aquellos que pudiesen aparecer en las condiciones iniciales y de
contorno adimensionalizadas. Esto significa que la dependencia de
la solución con respecto a los parámetros que intervienen en el
problema ha podido ser simplificada de forma notable, y que, una
vez obtenida la solución en forma adimensional para un conjunto
determinado de valores de los parámetros que intervienen, dicha
solución permitirá determinar la solución correspondiente a
cualquier otro conjunto de valores de parámetros siempre que éstos
proporcionen los mismos valores de los números adimensionales que
aquellos para los que fue obtenida la solución adimensional. Éste
es un resultado extraordinariamente útil también en mecánica de
fluidos experimental: la descripción de un flujo puede hacerse a
partir de los resultados de un experimento en el que las
condiciones sean semejantes a las que existen en dicho flujo. La
semejanza entre dos flujos queda precisamente garantizada por la
igualdad de los números adimensionales relevantes en el problema,
determinados a partir de los parámetros que definen las
condiciones que describen cada uno de los flujos.
De las ecuaciones (4.21) a (4.23), teniendo en cuenta que han sido obtenidas dividiendo los factores entre llaves de las ecuaciones (4.11) a (4.13) por el que aparece en el término convectivo de cada una de ellas, puede deducirse fácilmente el significado físico de cada una de los números adimensionales definidos en las ecuaciones (4.15) a (4.20).
El denominado número de Strouhal, St, expresa la
importancia relativa del término de variación local de cada una de
las ecuaciones (primer término) frente al correspondiente término
convectivo (segundo término). Obsérvese que si
St![]() ,
el primer término de cada ecuación puede despreciarse frente al
segundo, y el flujo puede generalmente considerarse
quasi-estacionario.4.3 Esto último significa que el tiempo
característico asociado a la no estacionareidad del movimiento,
,
el primer término de cada ecuación puede despreciarse frente al
segundo, y el flujo puede generalmente considerarse
quasi-estacionario.4.3 Esto último significa que el tiempo
característico asociado a la no estacionareidad del movimiento,
![]() , es mucho mayor que el tiempo que emplea una partícula
fluida en recorrer la longitud característica del problema,
, es mucho mayor que el tiempo que emplea una partícula
fluida en recorrer la longitud característica del problema,
![]() .4.4
.4.4
El número de Reynolds, Re, expresa la relación entre los
órdenes de magnitud de los términos convectivo y viscoso en la
ecuación de conservación de la cantidad de movimiento. Establece,
por tanto, el orden de magnitud relativo de las fuerzas de inercia
debidas a la aceleración convectiva frente a las fuerzas debidas a
la viscosidad que actúan sobre el fluido. Cuando el número de
Reynolds es suficientemente grande (según el tipo de flujo, Re
puede tomar desde valores próximos a cero hasta valores del orden
de ![]() o incluso superiores,4.5 el término viscoso de la ecuación de conservación de la
cantidad de movimiento tiende a anularse (excepto en determinadas
zonas del campo fluido, según se discutirá más adelante).***
o incluso superiores,4.5 el término viscoso de la ecuación de conservación de la
cantidad de movimiento tiende a anularse (excepto en determinadas
zonas del campo fluido, según se discutirá más adelante).***
El cuadrado del número de Froude, (Fr)![]() , expresa la
relación entre los términos que representan las fuerzas de inercia
debidas a la aceleración convectiva y las fuerzas gravitatorias en
la ecuación de conservación de la cantidad de movimiento.
Obsérvese que el último término de la ecuación (4.22),
que representa la contribución de las fuerzas gravitatorias en el
balance de cantidad de movimiento de la partícula fluida, puede
despreciarse cuando el número de Froude es suficientemente grande.
En el estudio de flujos con superficie libre4.6 el número de Froude es
importante. En este tipo de flujos, la acción de la gravedad
consigue mantener la superficie libre horizontal sólo cuando el
número de Froude es suficientemente bajo, en cuyo caso puede
despreciarse la resistencia al movimiento de un cuerpo que flote
sobre la superficie libre, asociada a la generación de olas.
, expresa la
relación entre los términos que representan las fuerzas de inercia
debidas a la aceleración convectiva y las fuerzas gravitatorias en
la ecuación de conservación de la cantidad de movimiento.
Obsérvese que el último término de la ecuación (4.22),
que representa la contribución de las fuerzas gravitatorias en el
balance de cantidad de movimiento de la partícula fluida, puede
despreciarse cuando el número de Froude es suficientemente grande.
En el estudio de flujos con superficie libre4.6 el número de Froude es
importante. En este tipo de flujos, la acción de la gravedad
consigue mantener la superficie libre horizontal sólo cuando el
número de Froude es suficientemente bajo, en cuyo caso puede
despreciarse la resistencia al movimiento de un cuerpo que flote
sobre la superficie libre, asociada a la generación de olas.
El número de Mach, M, expresa la relación entre la
velocidad del fluido ![]() y la velocidad de propagación del
sonido en el fluido
y la velocidad de propagación del
sonido en el fluido
![]() , y proporciona una
medida de la importancia de los efectos de compresibilidad en el
flujo.4.7Si la velocidad típica del fluido es suficientemente pequeña
frente a la velocidad del sonido, las variaciones relativas de
densidad debidas a variaciones de presión en el flujo serán muy
pequeñas.
, y proporciona una
medida de la importancia de los efectos de compresibilidad en el
flujo.4.7Si la velocidad típica del fluido es suficientemente pequeña
frente a la velocidad del sonido, las variaciones relativas de
densidad debidas a variaciones de presión en el flujo serán muy
pequeñas.
El número de Prandtl, Pr, expresa la relación entre la
difusividad de cantidad de movimiento (o viscosidad cinemática),
![]() , y la difusividad térmica,
, y la difusividad térmica,
![]() . Obsérvese que esta relación
viene dada por el cociente de los factores entre llaves que
afectan a los términos de difusión de cantidad de movimiento y de
conducción de calor de las ecuaciones (4.12) y
(4.13). Pr es de orden unidad en gases. En agua,
Pr
. Obsérvese que esta relación
viene dada por el cociente de los factores entre llaves que
afectan a los términos de difusión de cantidad de movimiento y de
conducción de calor de las ecuaciones (4.12) y
(4.13). Pr es de orden unidad en gases. En agua,
Pr![]() a 15
a 15![]() C, y disminuye rápidamente al aumentar
la temperatura. En metales líquidos como el mercurio y el sodio,
Pr es mucho menor que la unidad.
C, y disminuye rápidamente al aumentar
la temperatura. En metales líquidos como el mercurio y el sodio,
Pr es mucho menor que la unidad.
Si se adimensionaliza también la ecuación (3.16), pueden introducirse otros dos números adimensionales análogos al número de Prandtl: el número de Schmidt,
Debe observarse que, a diferencia de lo que ocurre con los números de Reynolds, Strouhal, Froude y Mach (entre otros), que dependen de las condiciones del flujo, los números de Prandtl, Schmidt y Lewis se determinan exclusivamente a partir de propiedades del fluido que dependen del estado termodinámico para el que se evalúen.
Existen bastantes más números adimensionales que los que se acaba
de comentar, que aparecen en problemas en los que intervienen, por
ejemplo, fenómenos de tensión superficial (número de Weber, We),
procesos de transmisión de calor por convección natural (número de
Grashof, Gr, o de Rayleigh,
Ra![]() Gr
Gr![]() Pr
Pr![]() ),
transmisión de calor entre fluidos en movimiento y sólidos (número
de Nusselt, Nu), etc. También suelen utilizarse números
adimensionales que son combinaciones de otros ya mencionados aquí,
tales como el número de Peclet
(
Pe
),
transmisión de calor entre fluidos en movimiento y sólidos (número
de Nusselt, Nu), etc. También suelen utilizarse números
adimensionales que son combinaciones de otros ya mencionados aquí,
tales como el número de Peclet
(
Pe![]() Re
Re![]() Pr
Pr![]() ). Una descripción más
detallada de los números adimensionales más importantes y de
problemas en los que intervienen puede encontrarse en algunas de
las referencias indicadas al final del texto. También pueden consultarse
estas referencias para estudiar conceptos y métodos que facilitan
el análisis dimensional, en particular el teorema
). Una descripción más
detallada de los números adimensionales más importantes y de
problemas en los que intervienen puede encontrarse en algunas de
las referencias indicadas al final del texto. También pueden consultarse
estas referencias para estudiar conceptos y métodos que facilitan
el análisis dimensional, en particular el teorema ![]() de
Buckingham, que permite simplificar de forma sistemática la
relación funcional entre los diversos parámetros que intervienen
en un problema dado. En cualquier caso, la mejor forma de aplicar
el análisis dimensional a un problema, y particularmente si lo que
se pretende es llevar a cabo posteriormente un estudio numérico,
es el basado en la adimensionalización de las ecuaciones de
conservación y condiciones de contorno, que deben incluir todos
los términos necesarios para la descripción apropiada del flujo.
Aunque la discusión que se ha presentado en este capítulo ha sido
necesariamente muy breve, es importante comprender los conceptos
básicos y la utilidad del análisis dimensional en mecánica de
fluidos.
de
Buckingham, que permite simplificar de forma sistemática la
relación funcional entre los diversos parámetros que intervienen
en un problema dado. En cualquier caso, la mejor forma de aplicar
el análisis dimensional a un problema, y particularmente si lo que
se pretende es llevar a cabo posteriormente un estudio numérico,
es el basado en la adimensionalización de las ecuaciones de
conservación y condiciones de contorno, que deben incluir todos
los términos necesarios para la descripción apropiada del flujo.
Aunque la discusión que se ha presentado en este capítulo ha sido
necesariamente muy breve, es importante comprender los conceptos
básicos y la utilidad del análisis dimensional en mecánica de
fluidos.
Ejemplo 1: Un depósito de grandes dimensiones
contiene un líquido de densidad ![]() y viscosidad
y viscosidad ![]() sobre
cuya superficie libre, situada a una altura
sobre
cuya superficie libre, situada a una altura ![]() sobre el fondo,
existe una presión manométrica
sobre el fondo,
existe una presión manométrica ![]() . El líquido se descarga
a la atmósfera a través de una tubería lisa horizontal, de
longitud
. El líquido se descarga
a la atmósfera a través de una tubería lisa horizontal, de
longitud ![]() y sección circular de diámetro
y sección circular de diámetro ![]() , conectada al
fondo del depósito. Mediante análisis dimensional, se trata de
simplificar la dependencia funcional del caudal de descarga,
, conectada al
fondo del depósito. Mediante análisis dimensional, se trata de
simplificar la dependencia funcional del caudal de descarga, ![]() ,
con los parámetros que intervienen en el problema.
,
con los parámetros que intervienen en el problema.
Si suponemos que el flujo es quasi-estacionario al ser el depósito muy grande, las ecuaciones que describen el flujo son las siguientes:
| (4.27) |
Ejemplo 2: Supóngase un canal
vertical formado por dos placas planas y paralelas, una de las
cuales se mantiene a una temperatura uniforme, ![]() , siendo la
otra adiabática. La altura del canal es
, siendo la
otra adiabática. La altura del canal es ![]() y la separación
entre placas,
y la separación
entre placas, ![]() . El problema se considerará bidimensional y
estacionario. Se trata de estudiar el flujo de un gas perfecto
inducido por flotación en el canal, que se supondrá que puede
describirse mediante las correspondientes ecuaciones de
conservación de la masa, cantidad de movimiento y energía interna,
en las que la densidad, la viscosidad y la conductividad térmica
se considerarán variables. Demuéstrese que a partir de dichas
ecuaciones es posible deducir las siguientes ecuaciones en forma
adimensional (
. El problema se considerará bidimensional y
estacionario. Se trata de estudiar el flujo de un gas perfecto
inducido por flotación en el canal, que se supondrá que puede
describirse mediante las correspondientes ecuaciones de
conservación de la masa, cantidad de movimiento y energía interna,
en las que la densidad, la viscosidad y la conductividad térmica
se considerarán variables. Demuéstrese que a partir de dichas
ecuaciones es posible deducir las siguientes ecuaciones en forma
adimensional (![]() e
e ![]() son las coordenadas en dirección vertical
y transversal al canal, respectivamente; se tomará el origen de
son las coordenadas en dirección vertical
y transversal al canal, respectivamente; se tomará el origen de
![]() en el extremo inferior del canal, y el de
en el extremo inferior del canal, y el de ![]() en la placa
caliente):
en la placa
caliente):
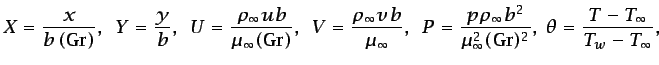 |
(4.35) |
Como condiciones de contorno se supondrá que pueden imponerse las
siguientes: En las paredes, la condición de no deslizamiento; una
temperatura fija en la pared caliente, igual a ![]() (
(![]() ),
y un flujo de calor nulo en la pared adiabática
(
),
y un flujo de calor nulo en la pared adiabática
(
![]() ). En la sección de salida
(
). En la sección de salida
(
![]() Gr
Gr![]() ), se fijará
), se fijará ![]() y se supondrán
despreciables las variaciones de las magnitudes fluidas en la
dirección del eje
y se supondrán
despreciables las variaciones de las magnitudes fluidas en la
dirección del eje ![]() . En la sección de entrada al canal (
. En la sección de entrada al canal (![]() ),
se supondrá que el flujo másico depende de la raíz cuadrada de la
diferencia entre la presión ambiente (en el exterior del canal) y
la presión en la sección de entrada (equivalente a aplicar la
ecuación de Bernoulli entre un punto en el exterior del canal,
alejado de la sección de entrada, y cualquier punto de ésta); en
la ecuación de la energía, puede suponerse que no hay flujo de
calor por conducción a través de la sección de entrada, y que el
fluido entrante tiene la temperatura ambiente
),
se supondrá que el flujo másico depende de la raíz cuadrada de la
diferencia entre la presión ambiente (en el exterior del canal) y
la presión en la sección de entrada (equivalente a aplicar la
ecuación de Bernoulli entre un punto en el exterior del canal,
alejado de la sección de entrada, y cualquier punto de ésta); en
la ecuación de la energía, puede suponerse que no hay flujo de
calor por conducción a través de la sección de entrada, y que el
fluido entrante tiene la temperatura ambiente ![]() .
.
De las ecuaciones (4.31) a (4.34), (4.37) y (4.38) y las condiciones de contorno, se deduce que la solución, y en particular el número de Nusselt
![$\displaystyle =\frac{b(\mbox{Gr})}{L_{c}}\int^{L_{c}/[b
(\mbox{\scriptsize Gr})]}_{0}{\mbox{Nu}_{x} \mbox{d}X},
$](img509.gif)