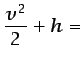Flujo ideal

Los flujos compresibles de fluidos con viscosidad y conductividad térmica despreciables se describen mediante las ecuaciones (5.55), (5.56) y (5.57) de Euler. Si además el flujo es estacionario, homentrópico^5.35 e irrotacional, y las fuerzas másicas son despreciables, se satisface la ecuación (5.71) y la constante es la misma para todas las líneas de corriente,

$$\frac{v^2}{2} + h = .$$ (5.128)

Al ser el flujo irrotacional, es posible definir un potencial de velocidad, de forma que

$$\vec{v}=\vec{\nabla}\phi.$$ (5.129)

De las ecuaciones (5.36) y (5.126) se deduce

$$\rho = \frac{\rho}{c^2} h,$$ (5.130)

e introduciendo esta expresión en la ecuación (5.55) de conservación de la masa, teniendo en cuenta la ecuación (5.129) (que además permite expresar $\vec{\nabla}\cdot\vec{v}=\nabla^2\phi$), y que el flujo se está suponiendo estacionario, se obtiene

$$\frac{1}{c^2} \vec{\nabla}\phi\cdot\vec{\nabla}h + \nabla^2\phi=0.$$ (5.131)

Haciendo uso de la ecuación (5.128), la ecuación (5.131) puede expresarse finalmente de la siguiente forma:

$$\frac{1}{c^2} \vec{\nabla}\phi\cdot\vec{\nabla}\left[\frac{1}{2}(\vec{\nabla}\phi)^2\right] = \nabla^2\phi,$$ (5.132)

o bien, en notación de subíndices,

$$\frac{1}{c^2}\frac{\partial \phi}{\partial x_i}\frac{\partial \ph... ...al^2 \phi}{\partial x_i \partial x_j} = \frac{\partial^2 \phi}{\partial x_i^2}.$$ (5.133)

Para un gas caloríficamente perfecto, para el que la velocidad del sonido definida en la ecuación (5.126) resulta

$$c=(\gamma R T)^{1/2},$$ (5.134)

y $h=c_p T$, a partir de la ecuación (5.128) se deduce la siguiente relación entre el módulo del vector velocidad y $c$:

$$\frac{\gamma-1}{2} v^2 + c^2 = c_0^2,$$ (5.135)

y teniendo en cuenta la ecuación (5.129),

$$\frac{\gamma-1}{2}\left(\vec{\nabla}\phi\right)^2 + c^2 = c_0^2,$$ (5.136)

donde $c_0$ es la velocidad del sonido en condiciones de remanso.^5.36Introduciendo la ecuación (5.136) en la ecuación (5.133), se obtiene una ecuación que permite determinar $\phi$. Dicha ecuación, junto con las ecuaciones (5.129) y (5.136),^5.37 permiten describir flujos estacionarios subsónicos ($M<1$), transónicos ( $M\approx 1$) o supersónicos ($M>1$), cuando son aceptables las aproximaciones introducidas. En lugar de la ecuación que resulta de introducir la ecuación (5.136) en la ecuación (5.133), que es altamente no lineal, suele resolverse en realidad el sistema formado por la ecuación que resulta de sustituir $(\partial \phi/\partial x_i)(\partial \phi/\partial x_j)$ por $v_i v_j$ en la ecuación (5.133),

$$\begin{split}\left(1 -\frac{v_1^2}{c^2}\right)&\frac{\partial... ...artial^2 \phi}{\partial x_1 \partial x_3}\right)=0, \end{split}$$ (5.137)

junto con las ecuaciones (5.129) y (5.135).

Para cuerpos aerodinámicos delgados dispuestos paralelamente a un flujo incidente de velocidad uniforme, las ecuaciones (5.133) y (5.135) pueden linealizarse si se supone que el cuerpo sólo introduce pequeñas perturbaciones en la velocidad del flujo incidente,^5.38lo que da lugar a una forma más simple de la ecuación (5.137), que en los casos de flujos subsónicos o supersónicos puede quedar reducida a la ecuación lineal^5.39

$$(1-M_\infty^2)\frac{\partial^2 \phi}{\partial x_1^2} + \frac{\partial^2 \phi}{\partial x_2^2} + \frac{\partial^2 \phi}{\partial x_3^2}=0,$$ (5.138)

que, como se observa, es muy parecida a la ecuación de Laplace (5.9) que describe los flujos potenciales de fluidos incompresibles.

En algunos problemas en los que existen zonas de flujo supersónico (la velocidad del fluido es superior a la velocidad local del sonido), pueden aparecer superficies de discontinuidad a través de las cuales se producen saltos de magnitudes fluidas, denominadas ondas de choque, que introducen una dificultad adicional en el procedimiento numérico de resolución. Las ondas de choque pueden ser móviles (como las que se producen en explosiones) o estacionarias (como las que pueden aparecer en el flujo estacionario a través de toberas convergentes-divergentes); normales (la onda de choque es normal al flujo a través de ella) u oblicuas; fuertes (el flujo incidente relativo a la onda es supersónico y, el flujo detrás de ella es siempre subsónico) o débiles (en ondas oblicuas, aunque la componente de la velocidad normal a la onda, detrás de ésta, corresponde a un flujo subsónico, el flujo puede resultar supersónico debido a la componente tangencial). En una onda de choque, los efectos de la viscosidad y la conductividad térmica dan lugar a fenómenos disipativos que producen un aumento de entropía a través de la onda. Lo que ocurre es que las ecuaciones de Euler no permiten en ciertos casos, definidos por condiciones de contorno determinadas, proporcionar una solución isentrópica en todo el campo fluido. Sin embargo, si las condiciones de aplicabilidad de la teoría ideal se cumplen, el tamaño de la onda de choque, en la que existirán elevados gradientes de las magnitudes fluidas y los fenómenos de transporte no pueden despreciarse, será muy pequeño en comparación con la longitud característica del problema. De hecho, las ondas de choque son tratadas generalmente como superficies de discontinuidad. Las condiciones de salto través de ellas, denominadas condiciones de Rankine-Hugoniot, se determinan aplicando las ecuaciones de conservación de la masa, de la cantidad de movimiento y de la energía, teniendo en cuenta que la entropía del fluido debe aumentar al atravesar la onda de choque.^5.40 Las siguientes relaciones determinan el salto de propiedades a través de una onda de choque normal para un gas perfecto:^5.41

$$\frac{\rho_{2}}{\rho_{1}}=\frac{v_{1}}{v_{2}}= \frac{(\gamma+1)M_{1}^{2}}{(\gamma-1)M_{1}^{2}+2},$$ (5.139)

$$\frac{p_{2}}{p_{1}}=\frac{1}{\gamma+1} [2\gamma M_{1}^{2}-(\gamma-1)],$$ (5.140)

$$\frac{T_{2}}{T_{1}}=\left(\frac{c_{2}}{c_{1}}\right)^{2}=\frac{[2\gamma M_{1}^{2}-(\gamma-1)][(\gamma-1)M_{1}^{2}+2]}{(\gamma+1)^{2}M_{1}^{2}},$$ (5.141)

$$M_{2}^{2}=\frac{(\gamma-1)M_{1}^{2}+2}{2\gamma M_{1}^{2}-(\gamma-1)}.$$ (5.142)

La disminución de la presión de remanso a través de una onda de choque normal viene dada por

$$\frac{p_{01}}{p_{02}}=\left\{\frac{2\gamma M_{1}^{2}-(\gamma-1)}{... ..._{1}^{2}+2} {(\gamma+1)M_{1}^{2}}\right]^{\gamma}\right\}^{\frac{1}{\gamma-1}}.$$ (5.143)

La entalpía de remanso se conserva a través de la onda de choque. Obsérvese que la intensidad de la onda de choque aumenta con $M_1$.

En flujos en los que no existen ondas de choque (o éstas son débiles) es mucho más eficiente resolver el sistema formado por las ecuaciones (5.133), (5.129) y (5.136) que las ecuaciones (5.55), (5.56) y (5.57) para las variables primitivas ( $\vec{v},\rho,p$) (Fletcher, 1991). Las ecuaciones (5.129), (5.133) y (5.136) suelen aplicarse en la resolución numérica de flujos alrededor de perfiles aerodinámicos con ángulos de ataque pequeños, para los que no exista separación de la capa límite.

En flujos supersónicos con ondas de choque, es posible utilizar las ecuaciones (5.139) a (5.143) para calcular la variación de las magnitudes fluidas a través de las ondas, en combinación con esquemas numéricos adecuados para flujos sin ondas de choque. Sin embargo, cuando no se conoce a priori la localización de las ondas de choque, este enfoque resulta poco efectivo. Es preferible obtener soluciones que satisfagan la denominada formulación débil de las ecuaciones de conservación (que se tratará en capítulos posteriores), ya que dichas soluciones satisfacen también las condiciones de salto de Rankine-Hugoniot, prediciendo adecuadamente, por tanto, la intensidad y localización de las ondas de choque.