



Next: Ecuaciones generales de la
Up: Cinemática de fluidos
Previous: Análisis del movimiento relativo
Índice General
Circulación. Movimientos irrotacionales
La circulación del vector velocidad a lo largo de una línea 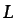 definida en el seno de un fluido se define como
definida en el seno de un fluido se define como
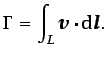 |
(2.22) |
Cuando la línea 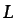 es cerrada, aplicando el teorema de Stokes
resulta
es cerrada, aplicando el teorema de Stokes
resulta
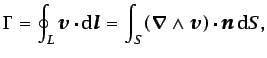 |
(2.23) |
siendo 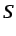 una superficie cualquiera que se apoya en
una superficie cualquiera que se apoya en 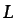 y
y
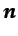 el vector unitario normal a cada elemento de superficie,
con sentido positivo hacia el lado de la superficie desde el que
se ve recorrer la línea
el vector unitario normal a cada elemento de superficie,
con sentido positivo hacia el lado de la superficie desde el que
se ve recorrer la línea 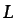 en el sentido opuesto al de las agujas
del reloj. Es importante destacar que
en el sentido opuesto al de las agujas
del reloj. Es importante destacar que 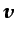 debe estar
definida y ser continua en un dominio que contenga
debe estar
definida y ser continua en un dominio que contenga 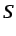 .
.
Si la circulación a lo largo de cualquier línea cerrada es nula,
el vector vorticidad,
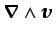 , es nulo en todo
el campo fluido, como resulta obvio si se toma una línea cerrada
tan pequeña como se quiera alrededor de cada punto y se aplica la
ecuación (2.23). El recíproco (
, es nulo en todo
el campo fluido, como resulta obvio si se toma una línea cerrada
tan pequeña como se quiera alrededor de cada punto y se aplica la
ecuación (2.23). El recíproco (
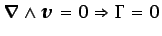 ) es en general cierto sólo si el dominio en
el que tiene lugar el flujo es simplemente conexo. Un dominio es
simplemente conexo si es posible encontrar, para cualquier línea
cerrada
) es en general cierto sólo si el dominio en
el que tiene lugar el flujo es simplemente conexo. Un dominio es
simplemente conexo si es posible encontrar, para cualquier línea
cerrada 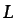 , una superficie que se apoye en
, una superficie que se apoye en 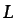 y esté
íntegramente contenida en el campo fluido. No es simplemente
conexo, por ejemplo, el campo fluido alrededor de una superficie
toroidal. En un movimiento plano, no es simplemente conexo un
campo fluido que contenga un sólido inmerso.
y esté
íntegramente contenida en el campo fluido. No es simplemente
conexo, por ejemplo, el campo fluido alrededor de una superficie
toroidal. En un movimiento plano, no es simplemente conexo un
campo fluido que contenga un sólido inmerso.
Como se verá más adelante, a los flujos en los
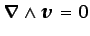 se les denomina flujos
irrotacionales.
se les denomina flujos
irrotacionales.
Es fácil demostrar que la derivada temporal de la circulación a lo
largo de una línea fluida cerrada2.11 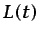 es igual a la circulación de la
aceleración a lo largo de
es igual a la circulación de la
aceleración a lo largo de 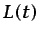 :
:
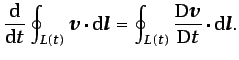 |
(2.24) |
Si la aceleración deriva de un potencial, se deduce de esta
expresión que su circulación es nula, y, por tanto, que la
derivada temporal de la circulación de la velocidad a lo largo de
cualquier línea fluida cerrada es nula. Esto quiere decir que, si
el flujo es inicialmente irrotacional, seguirá siéndolo en todo
instante. Es interesante, por tanto, conocer en qué condiciones la
aceleración deriva de un potencial,2.12 pero para ello será necesario deducir antes la
ecuación de conservación de la cantidad de movimiento, lo que se
hará en la Sección 3.3.




Next: Ecuaciones generales de la
Up: Cinemática de fluidos
Previous: Análisis del movimiento relativo
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![]() definida en el seno de un fluido se define como
definida en el seno de un fluido se define como
![]() , es nulo en todo
el campo fluido, como resulta obvio si se toma una línea cerrada
tan pequeña como se quiera alrededor de cada punto y se aplica la
ecuación (2.23). El recíproco (
, es nulo en todo
el campo fluido, como resulta obvio si se toma una línea cerrada
tan pequeña como se quiera alrededor de cada punto y se aplica la
ecuación (2.23). El recíproco (
![]() ) es en general cierto sólo si el dominio en
el que tiene lugar el flujo es simplemente conexo. Un dominio es
simplemente conexo si es posible encontrar, para cualquier línea
cerrada
) es en general cierto sólo si el dominio en
el que tiene lugar el flujo es simplemente conexo. Un dominio es
simplemente conexo si es posible encontrar, para cualquier línea
cerrada ![]() , una superficie que se apoye en
, una superficie que se apoye en ![]() y esté
íntegramente contenida en el campo fluido. No es simplemente
conexo, por ejemplo, el campo fluido alrededor de una superficie
toroidal. En un movimiento plano, no es simplemente conexo un
campo fluido que contenga un sólido inmerso.
y esté
íntegramente contenida en el campo fluido. No es simplemente
conexo, por ejemplo, el campo fluido alrededor de una superficie
toroidal. En un movimiento plano, no es simplemente conexo un
campo fluido que contenga un sólido inmerso.
![]() se les denomina flujos
irrotacionales.
se les denomina flujos
irrotacionales.
![]() es igual a la circulación de la
aceleración a lo largo de
es igual a la circulación de la
aceleración a lo largo de ![]() :
: