



Next: Ecuación de la vorticidad
Up: Forma diferencial
Previous: Leyes constitutivas de fluidos
Índice General
Ecuaciones de Navier-Stokes
Introduciendo la ley de Navier-Poisson de la ecuación (3.27)
en la ecuación (3.21) de conservación de la cantidad
de movimiento, sustituyendo previamente en ésta la descomposición
de la ecuación (3.25), se obtienen las ecuaciones de
Navier-Stokes:
![\begin{displaymath}\begin{split}\rho\left(\frac{\partial v_i}{\partial t} + v_j\...
...mu)\vec{\nabla}\cdot\vec{v}\right] +\rho f_{m_{i}}. \end{split}\end{displaymath}](img307.gif) |
(3.30) |
En notación vectorial,
![$\displaystyle \boxed{\rho \frac{\mbox{D}\vec {v}}{\mbox{D}t}=-\vec {\nabla}p +...
...left[(\mu_v-\frac{2}{3}\mu)\vec {\nabla}\cdot \vec {v}\right]+ \rho\vec {f}_m,}$](img308.gif) |
(3.31) |
siendo
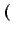 def def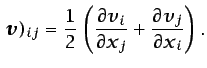 |
(3.32) |
Suponiendo que los coeficientes de viscosidad son uniformes, la
ecuación (3.31) puede escribirse como
sigue:3.10
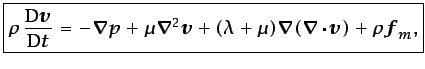 |
(3.33) |
donde
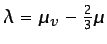 , y teniendo en cuenta la
identidad vectorial
, y teniendo en cuenta la
identidad vectorial
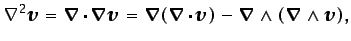 |
(3.34) |
y la definición del vector vorticidad de la Sección 2.4,
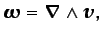 |
(3.35) |
se obtiene
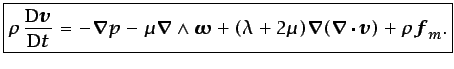 |
(3.36) |
Cuando el fluido puede considerarse incompresible, la ecuación
(3.33), teniendo en cuenta la ecuación (3.11),
se reduce a
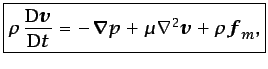 |
(3.37) |
o en notación tensorial,
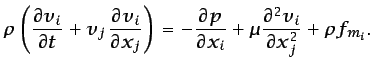 |
(3.38) |
Con la misma hipótesis de flujo incompresible, la ecuación
(3.36) queda como sigue:
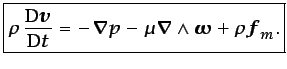 |
(3.39) |
Obsérvese que en la ecuación (3.39) desaparece el
término viscoso cuando el flujo es irrotacional, con lo que la
ecuación se reduce a la correspondiente a un fluido ideal (sin
viscosidad).3.11 Es decir, un fluido
viscoso incompresible se comporta como un fluido ideal en zonas
del campo fluido en las que
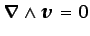 .
.




Next: Ecuación de la vorticidad
Up: Forma diferencial
Previous: Leyes constitutivas de fluidos
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![\begin{displaymath}\begin{split}\rho\left(\frac{\partial v_i}{\partial t} + v_j\...
...mu)\vec{\nabla}\cdot\vec{v}\right] +\rho f_{m_{i}}. \end{split}\end{displaymath}](img307.gif)