



Next: Flujo de Couette
Up: Aproximaciones basadas en consideraciones
Previous: Flujos estacionarios
Índice General
Flujos con efectos de viscosidad dominantes
La presencia del término convectivo, no lineal,
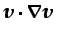 , en la ecuación de conservación de la
cantidad de movimiento introduce una gran dificultad en la
resolución de las ecuaciones de conservación. En algunos problemas
de interés dicho término es pequeño, y si el flujo es además
estacionario, o en todo caso
, en la ecuación de conservación de la
cantidad de movimiento introduce una gran dificultad en la
resolución de las ecuaciones de conservación. En algunos problemas
de interés dicho término es pequeño, y si el flujo es además
estacionario, o en todo caso
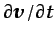 es
también suficientemente pequeño, puede ser aceptable la
aproximación que supone despreciar el término de inercia que
aparece en el primer miembro de la ecuación de conservación de la
cantidad de movimiento frente a los términos debidos a la presión
y a las fuerzas debidas a la viscosidad. En lo que sigue
supondremos además que el fluido es incompresible y de viscosidad
uniforme. La ecuación (5.39),
es
también suficientemente pequeño, puede ser aceptable la
aproximación que supone despreciar el término de inercia que
aparece en el primer miembro de la ecuación de conservación de la
cantidad de movimiento frente a los términos debidos a la presión
y a las fuerzas debidas a la viscosidad. En lo que sigue
supondremos además que el fluido es incompresible y de viscosidad
uniforme. La ecuación (5.39),
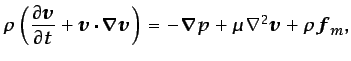 |
(5.76) |
queda por tanto de la forma siguiente:
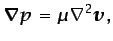 |
(5.77) |
donde, tal como se ha hecho en alguna ocasión anterior, se ha
supuesto que las fuerzas másicas derivan de un potencial y 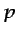 se
ha redefinido como presión reducida (véase la ecuación
(5.42)). La ecuación de conservación de la masa es
obviamente
se
ha redefinido como presión reducida (véase la ecuación
(5.42)). La ecuación de conservación de la masa es
obviamente
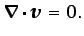 |
(5.78) |
La aproximación introducida en la ecuación (5.77) al
despreciar las fuerzas de inercia frente a las debidas a la
viscosidad puede ser aceptable si el número de Reynolds es
suficientemente pequeño:5.19
Re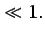 |
(5.79) |
Si en las condiciones de contorno que especifican la
causa que genera el movimiento del fluido sólo interviene
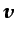 , el problema se reduce a resolver las ecuaciones
, el problema se reduce a resolver las ecuaciones
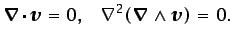 |
(5.80) |
La segunda igualdad en la ecuación (5.80) se obtiene
tomando el rotacional de la ecuación (5.77).5.20Obsérvese que la distribución de 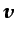 no dependerá de
no dependerá de 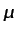 . La distribución de presión puede
obtenerse a partir de la ecuación (5.77).
. La distribución de presión puede
obtenerse a partir de la ecuación (5.77).
Si las condiciones de contorno que especifican la causa que genera
el movimiento del fluido se imponen sólo sobre 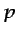 , el problema se
reduce a resolver la ecuación
, el problema se
reduce a resolver la ecuación
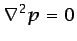 |
(5.81) |
(que se deduce tomando la divergencia en la ecuación
(5.77)). Obsérvese que la distribución de 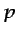 no
dependerá de
no
dependerá de 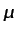 . La distribución de velocidad se deduce a
partir de la ecuación (5.77), teniendo en cuenta la
ecuación (5.78).
. La distribución de velocidad se deduce a
partir de la ecuación (5.77), teniendo en cuenta la
ecuación (5.78).
Debe tenerse en cuenta que el término
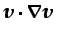 puede ser despreciable en la
ecuación (5.76) no solamente cuando
Re
puede ser despreciable en la
ecuación (5.76) no solamente cuando
Re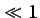 .
Por ejemplo, en un flujo de un fluido de densidad
.
Por ejemplo, en un flujo de un fluido de densidad 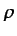 y
viscosidad
y
viscosidad 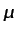 que circula con velocidad media
que circula con velocidad media 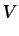 a través de
un conducto de longitud
a través de
un conducto de longitud 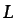 y sección de paso de tamaño
y sección de paso de tamaño 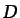 , es
fácil demostrar5.21 que
el término convectivo es despreciable si se satisface la condición
, es
fácil demostrar5.21 que
el término convectivo es despreciable si se satisface la condición
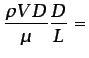 Re Re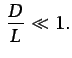 |
(5.82) |
Obsérvese que esta condición puede satisfacerse aun siendo Re de
orden unidad, o incluso muy superior,5.22 si 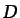 es suficientemente
pequeño frente a
es suficientemente
pequeño frente a 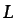 . Es decir, la unidireccionalidad del flujo,
favorecida con valores pequeños de la relación
. Es decir, la unidireccionalidad del flujo,
favorecida con valores pequeños de la relación 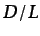 , contribuye a
que se satisfagan las condiciones necesarias para que los efectos
de viscosidad sean dominantes. Se hará referencia a continuación a
algunos ejemplos sencillos de flujos estacionarios y laminares de
fluidos incompresibles, con efectos de viscosidad dominantes. Los
dos primeros, flujos de Couette y de Hagen-Poiseuille, son flujos
unidireccionales (se supondrá que según la dirección de la
coordenada
, contribuye a
que se satisfagan las condiciones necesarias para que los efectos
de viscosidad sean dominantes. Se hará referencia a continuación a
algunos ejemplos sencillos de flujos estacionarios y laminares de
fluidos incompresibles, con efectos de viscosidad dominantes. Los
dos primeros, flujos de Couette y de Hagen-Poiseuille, son flujos
unidireccionales (se supondrá que según la dirección de la
coordenada 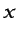 ). En estos flujos, el gradiente de presión reducida
no tiene componentes en dirección transversal al flujo y la
componente en la dirección del flujo, si existe, es constante, de
forma que la presión reducida varía linealmente con
). En estos flujos, el gradiente de presión reducida
no tiene componentes en dirección transversal al flujo y la
componente en la dirección del flujo, si existe, es constante, de
forma que la presión reducida varía linealmente con
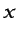 .5.23
.5.23
Subsecciones




Next: Flujo de Couette
Up: Aproximaciones basadas en consideraciones
Previous: Flujos estacionarios
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![]() , en la ecuación de conservación de la
cantidad de movimiento introduce una gran dificultad en la
resolución de las ecuaciones de conservación. En algunos problemas
de interés dicho término es pequeño, y si el flujo es además
estacionario, o en todo caso
, en la ecuación de conservación de la
cantidad de movimiento introduce una gran dificultad en la
resolución de las ecuaciones de conservación. En algunos problemas
de interés dicho término es pequeño, y si el flujo es además
estacionario, o en todo caso
![]() es
también suficientemente pequeño, puede ser aceptable la
aproximación que supone despreciar el término de inercia que
aparece en el primer miembro de la ecuación de conservación de la
cantidad de movimiento frente a los términos debidos a la presión
y a las fuerzas debidas a la viscosidad. En lo que sigue
supondremos además que el fluido es incompresible y de viscosidad
uniforme. La ecuación (5.39),
es
también suficientemente pequeño, puede ser aceptable la
aproximación que supone despreciar el término de inercia que
aparece en el primer miembro de la ecuación de conservación de la
cantidad de movimiento frente a los términos debidos a la presión
y a las fuerzas debidas a la viscosidad. En lo que sigue
supondremos además que el fluido es incompresible y de viscosidad
uniforme. La ecuación (5.39),
![]() , el problema se reduce a resolver las ecuaciones
, el problema se reduce a resolver las ecuaciones
![]() , el problema se
reduce a resolver la ecuación
, el problema se
reduce a resolver la ecuación
![]() puede ser despreciable en la
ecuación (5.76) no solamente cuando
Re
puede ser despreciable en la
ecuación (5.76) no solamente cuando
Re![]() .
Por ejemplo, en un flujo de un fluido de densidad
.
Por ejemplo, en un flujo de un fluido de densidad ![]() y
viscosidad
y
viscosidad ![]() que circula con velocidad media
que circula con velocidad media ![]() a través de
un conducto de longitud
a través de
un conducto de longitud ![]() y sección de paso de tamaño
y sección de paso de tamaño ![]() , es
fácil demostrar5.21 que
el término convectivo es despreciable si se satisface la condición
, es
fácil demostrar5.21 que
el término convectivo es despreciable si se satisface la condición