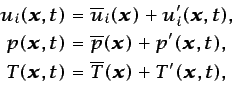Tratamiento estadístico de las ecuaciones en flujos turbulentos

Como implícitamente se ha indicado, la validez de las soluciones aproximadas que proporcionan las diferentes formas simplificadas de las ecuaciones de conservación está restringida a una serie de situaciones en las que determinados parámetros adimensionales varían dentro de un cierto rango. Sin embargo, en principio debe existir formalmente al menos una solución exacta estacionaria de las ecuaciones generales para cualquier tipo de problema en el que las condiciones de contorno sean estacionarias. No obstante, esto no quiere decir que tal solución corresponda a un flujo que necesariamente exista en la naturaleza, para lo cual la solución, además de satisfacer las ecuaciones, debe ser estable. De hecho, en la naturaleza y en la mayoría de las aplicaciones tecnológicas predominan los flujos turbulentos, en los que las magnitudes fluidas fluctúan de forma aparentemente aleatoria en el espacio y en el tiempo, incluso bajo condiciones de contorno estacionarias, y que aparecen como consecuencia de la inestabilidad (generalmente a altos números de Reynolds o de otros parámetros relevantes) de flujos laminares. El determinar si un flujo laminar dado es o no inestable, y si da lugar, en caso de que lo sea, a la aparición de otro flujo laminar estacionario (cuya unicidad no está garantizada) o a la transición a la turbulencia, es objeto de estudio de la teoría de la estabilidad hidrodinámica. El experimento de Reynolds es un ejemplo^5.27 de transición a la turbulencia del flujo de Hagen-Poiseuille, descrito en la Sección 5.4.3. Como ya se ha indicado, este tipo de flujos suele ser turbulento para números de Reynolds por encima de 2000. Aunque en una etapa inicial del proceso de transición a la turbulencia de la corriente laminar aparecen inestabilidades frente a pequeñas perturbaciones, una completa descripción de todo el proceso requiere la consideración del desarrollo de perturbaciones de amplitud finita, lo que representa una tarea muy complicada dado que ello conduce a problemas no lineales.

En flujos turbulentos completamente desarrollados, como ya se ha dicho, las propiedades varían con el tiempo, en cada punto del campo fluido, de una forma aleatoria en apariencia, siendo las amplitudes de las fluctuaciones, en general, comparables a los valores medios. El movimiento turbulento se caracteriza además por ser tridimensional y presentar altos niveles de vorticidad fluctuante, y por la existencia de multitud de escalas de longitud y tiempo, asociadas a torbellinos de distintos tamaños, en un rango comprendido entre las escalas correspondientes al mecanismo generador de la turbulencia y las disipativas (en las que la energía cinética de la turbulencia se transforma en energía térmica), lo que hace imposible un enfoque determinista y una descripción detallada del movimiento, a pesar de que, obviamente, el movimiento sigue estando descrito por las ecuaciones de Navier-Stokes.

Por ello suele recurrirse a la utilización de métodos estadísticos que proporcionen información acerca de la variación de valores medios de las magnitudes fluidas o de correlaciones entre fluctuaciones de éstas. La teoría estadística de la turbulencia tuvo su origen en el tratamiento de flujos turbulentos homogéneos e isótropos, en los que las fluctuaciones de presión y velocidad son estadísticamente independientes de la posición y de un cambio de orientación del sistema de referencia. En dichos métodos estadísticos, las magnitudes fluidas son consideradas variables estocásticas cuyos valores instantáneos pueden descomponerse en suma de un valor medio y un valor fluctuante:

$$\begin{split}u_i(\vec{x},t) & =\overline{u}_i(\vec{x}) + u'_i... ...vec{x},t) & =\overline{T}(\vec{x}) + T'(\vec{x},t), \end{split}$$ (5.91)

definiéndose los valores medios mediante

$$\overline{u}_i(\vec{x})=\lim_{t_0\rightarrow\infty} \frac{1}{t_0}\int_0^{t_0}u_i(\vec{x},t) t.$$ (5.92)

En realidad, las ecuaciones (5.91) y (5.92) son estrictamente válidas sólo cuando el flujo es estacionario. En caso contrario, los valores medios también dependerían del tiempo. No obstante, si la escala de tiempo asociada a las fluctuaciones turbulentas es mucho menor que la escala de tiempo característica en la que varían las magnitudes medias, $t_c$, el promediado de la ecuación (5.92) puede ser aceptable si se utiliza un valor suficientemente grande de $t_0$ (que permita promediar las fluctuaciones de cualquier frecuencia), que a la vez satisfaga la condición $t_0\ll t_c$. Puede consultarse, por ejemplo, el texto de Wilcox (1994) para un estudio detallado de modelos de turbulencia de tipo estadístico. Aquí nos limitaremos a introducir la descomposición de la ecuación (5.91) en las ecuaciones de conservación, y a poner de manifiesto que el promediado de dichas ecuaciones, utilizando la ecuación (5.92), da lugar a la aparición de correlaciones de segundo orden entre magnitudes fluctuantes, procedentes de los términos convectivos de las ecuaciones instantáneas, que pueden interpretarse como flujos turbulentos que se suman a los flujos correspondientes al transporte laminar de las magnitudes fluidas medias, siendo generalmente los segundos mucho menores que los primeros. En principio, las correlaciones de segundo orden entre magnitudes fluctuantes podrían determinarse a partir de las correspondientes ecuaciones de transporte para dichas correlaciones. Desafortunadamente, en estas ecuaciones de transporte, que pueden obtenerse mediante manipulación de las ecuaciones instantáneas y posterior promediado, aparecen nuevas correlaciones desconocidas entre magnitudes fluctuantes, de segundo y tercer orden. Esto constituye el denominado problema del cierre: en las ecuaciones de transporte para correlaciones de un determinado orden aparecen correlaciones de orden superior. La única forma de resolver esta dificultad consiste en la introducción de modelos que permitan expresar las correlaciones desconocidas en un determinado nivel de cierre en función de los valores medios de las magnitudes fluidas y de correlaciones de orden inferior.

En lo que sigue, consideraremos, para simplificar, flujos de fluidos incompresibles con propiedades constantes, descritos por las ecuaciones (3.12), (3.38) y (5.44):^5.28

$$\frac{\partial v_j}{\partial x_j}=0,$$ (5.93)

$$\rho\left(\frac{\partial v_i}{\partial t} + v_j \frac{\partial v... ...\partial x_j}\left(\mu\frac{\partial v_i}{\partial x_j}\right) +\rho f_{m_{i}},$$ (5.94)

$$\rho c_v\left(\frac{\partial T}{\partial t} + v_j \frac{\partial... ...rac{\partial}{\partial x_j} \left(\kappa\frac{\partial T}{\partial x_j}\right).$$ (5.95)

Introduciendo la descomposición de la ecuación (5.91) en las ecuaciones anteriores y promediando, se obtiene^5.29

$$\frac{\partial \overline{v}_j}{\partial x_j}=0,$$ (5.96)

$$\rho\left(\frac{\partial \overline{v}_i}{\partial t} + \overline{... ...\overline{v}_i}{\partial x_j} - \rho\overline{v'_iv'_j}\right) +\rho f_{m_{i}},$$ (5.97)

$$\rho c_v\left(\frac{\partial \overline{T}}{\partial t} + \overlin... ...\frac{\partial \overline{T}}{\partial x_j} - \rho c_v \overline{v'_jT'}\right).$$ (5.98)

Obsérvese que la ecuación promediada de conservación de la masa se obtiene de la instantánea sin más que sustituir la magnitud instantánea $v_j$ por la magnitud media $\overline{v}_j$. Con las ecuaciones de conservación de la cantidad de movimiento y la energía no ocurre lo mismo; además de sustituir magnitudes instantáneas por magnitudes medias, deben añadirse los términos $-\rho\overline{v'_iv'_j}$ y $-\rho c_v \overline{v'_jT'}$ dentro de la divergencia que aparece en los segundos miembros. Estos términos representan los ya mencionados flujos turbulentos de los valores medios de la cantidad de movimiento y de la energía, respectivamente, que proceden de los términos convectivos de las ecuaciones, y han sido agrupados en las ecuaciones (5.97) y (5.98) con los flujos de magnitudes fluidas medias debidos a la difusión con coeficientes de transporte laminar ($\mu$ y $\kappa$). La presencia de dichos términos en las ecuaciones se corresponde con la gran intensificación de los procesos de mezcla que se produce cuando en un flujo laminar tiene lugar la transición a flujo turbulento. En realidad, los flujos de difusión de las magnitudes medias con coeficientes de transporte molecular ( $\mu\partial \overline{v}_i/\partial x_j$ y $\kappa\partial \overline{T}/\partial x_j$) suelen ser despreciables frente a los flujos turbulentos ( $\rho\overline{v'_iv'_j}$ y $\rho c_v \overline{v'_jT'}$, respectivamente).^5.30 El tensor de segundo orden $\rho\overline{v'_iv'_j}$ queda definido por seis componentes, denominadas tensiones de Reynolds. El vector flujo turbulento de calor tiene obviamente tres componentes.

hit counter