



Next: Ecuación de conservación de
Up: Ecuación de conservación de
Previous: Forma diferencial
Índice General
Consideremos un fluido constituido por 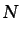 especies químicas. La
variación en el tiempo de la masa
especies químicas. La
variación en el tiempo de la masa 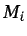 de la especie
de la especie 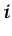 en un
volumen fluido
en un
volumen fluido 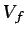 podrá deberse al transporte por difusión de
masa de dicha especie a través de la superficie que limita el
volumen fluido, o a la existencia de reacciones químicas:
podrá deberse al transporte por difusión de
masa de dicha especie a través de la superficie que limita el
volumen fluido, o a la existencia de reacciones químicas:
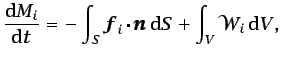 |
(3.13) |
siendo 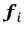 el vector flujo de masa de la especie
el vector flujo de masa de la especie 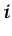 por
unidad de área que se introdujo en la ecuación (1.36) y
definido, por ejemplo, en la ecuación (1.40), y
por
unidad de área que se introdujo en la ecuación (1.36) y
definido, por ejemplo, en la ecuación (1.40), y
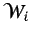 el ritmo de producción de masa de la especie
el ritmo de producción de masa de la especie 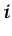 por unidad de volumen debida a reacciones químicas.
por unidad de volumen debida a reacciones químicas.
Haciendo
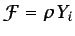 en la ecuación (3.3), siendo
en la ecuación (3.3), siendo
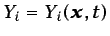 la fracción másica de la especie
la fracción másica de la especie 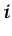 , y
teniendo en cuenta la ecuación (3.13), se obtiene la
siguiente ecuación de conservación de la fracción másica de la
especie
, y
teniendo en cuenta la ecuación (3.13), se obtiene la
siguiente ecuación de conservación de la fracción másica de la
especie 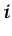 :
:
Dado que
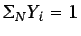 ,
,
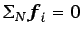 y
y
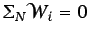 , al sumar las
, al sumar las 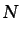 expresiones correspondientes a
la ecuación (3.14) para las
expresiones correspondientes a
la ecuación (3.14) para las 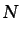 especies, se obtiene la
ecuación (3.4). Sólo serán necesarias, por tanto,
especies, se obtiene la
ecuación (3.4). Sólo serán necesarias, por tanto, 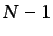 ecuaciones de conservación de la masa de otras tantas especies,
además de la ecuación de conservación de la masa
total,3.7 para obtener las distribuciones de las
ecuaciones de conservación de la masa de otras tantas especies,
además de la ecuación de conservación de la masa
total,3.7 para obtener las distribuciones de las 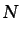 especies.
especies.
Análogamente a como se dedujo la ecuación (3.8) a partir
de la ecuación (3.4), de la ecuación (3.14) se
obtiene
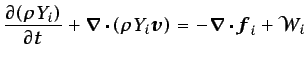 |
(3.15) |
(ecuación en forma conservativa). Teniendo en cuenta la ecuación
(3.8), y suponiendo que la difusión de masa puede
describirse mediante la ley de Fick expresada en la ecuación
(1.40), resulta
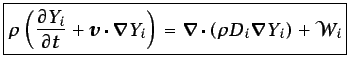 |
(3.16) |
(ecuación en forma no conservativa), siendo 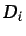 el coeficiente
de difusión de la especie
el coeficiente
de difusión de la especie 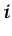 .
.




Next: Ecuación de conservación de
Up: Ecuación de conservación de
Previous: Forma diferencial
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![]() especies químicas. La
variación en el tiempo de la masa
especies químicas. La
variación en el tiempo de la masa ![]() de la especie
de la especie ![]() en un
volumen fluido
en un
volumen fluido ![]() podrá deberse al transporte por difusión de
masa de dicha especie a través de la superficie que limita el
volumen fluido, o a la existencia de reacciones químicas:
podrá deberse al transporte por difusión de
masa de dicha especie a través de la superficie que limita el
volumen fluido, o a la existencia de reacciones químicas:
![]() en la ecuación (3.3), siendo
en la ecuación (3.3), siendo
![]() la fracción másica de la especie
la fracción másica de la especie ![]() , y
teniendo en cuenta la ecuación (3.13), se obtiene la
siguiente ecuación de conservación de la fracción másica de la
especie
, y
teniendo en cuenta la ecuación (3.13), se obtiene la
siguiente ecuación de conservación de la fracción másica de la
especie ![]() :
: