Next: Condiciones iniciales y de
Up: Ecuaciones generales de la
Previous: Ecuación de la entropía
Índice General
Las ecuaciones (3.8), (3.31), (3.64)
y (3.16), junto con las ecuaciones de estado y
condiciones iniciales y de contorno apropiadas, describen el
movimiento tridimensional y no estacionario de un fluido
newtoniano, no homogéneo, compresible y viscoso:
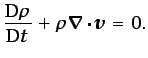 |
(3.70) |
![$\displaystyle \rho \frac{\mbox{D}\vec{v}}{\mbox{D}t}=-\vec{\nabla}p + 2\vec{\n...
...bla}\left[(\mu_v-\frac{2}{3}\mu)\vec{\nabla}\cdot\vec{v}\right]+ \rho\vec{f}_m,$](img363.gif) |
(3.71) |
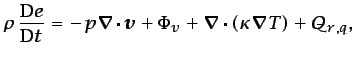 |
(3.72) |
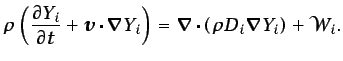 |
(3.73) |
Los términos
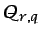 y
y
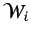 deben ser
modelados apropiadamente, lo que en general puede llegar a suponer
una gran dificultad. En lo que sigue se supondrá que el fluido
tiene un único componente, por lo que prescindiremos de las
ecuaciones de conservación de las especies, y que el término
deben ser
modelados apropiadamente, lo que en general puede llegar a suponer
una gran dificultad. En lo que sigue se supondrá que el fluido
tiene un único componente, por lo que prescindiremos de las
ecuaciones de conservación de las especies, y que el término
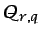 es conocido en función de
es conocido en función de 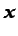 y
y 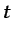 , o, en
todo caso, que puede expresarse en función de las variables
dependientes. Si tomamos
, o, en
todo caso, que puede expresarse en función de las variables
dependientes. Si tomamos 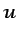 ,
, 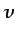 ,
, 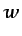 ,
, 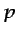 y
y 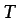 como las
variables dependientes, son necesarias las siguientes ecuaciones
adicionales para cerrar el sistema:
como las
variables dependientes, son necesarias las siguientes ecuaciones
adicionales para cerrar el sistema:
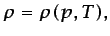 |
(3.74) |
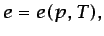 |
(3.75) |
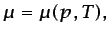 |
(3.76) |
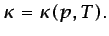 |
(3.77) |
Las ecuaciones (3.75) y (3.76) son las ecuaciones de
estado térmica y calórica, a las que ya se hizo referencia (en
particular para los casos de líquidos y gases perfectos) en la
Sección 1.4.2. Las ecuaciones3.15 (3.77) y (3.78) son
necesarias (generalmente, la dependencia suele ser sólo con
respecto a la temperatura, según se indicó anteriormente) salvo
que pueda considerarse que 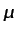 y
y 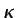 son constantes, lo
cual es aceptable en numerosas ocasiones. La fuerzas másicas
suelen ser datos del problema, aunque en el caso de las fuerzas de
Coriolis, por ejemplo, dependen de la velocidad del fluido. La
función de disipación
son constantes, lo
cual es aceptable en numerosas ocasiones. La fuerzas másicas
suelen ser datos del problema, aunque en el caso de las fuerzas de
Coriolis, por ejemplo, dependen de la velocidad del fluido. La
función de disipación
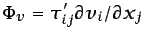 , y por tanto es también una función de las variables
dependientes.
, y por tanto es también una función de las variables
dependientes.
A las ecuaciones que forman el sistema de ecuaciones (3.71) a
(3.73) se les suele denominar frecuentemente, y por
extensión, ecuaciones de Navier-Stokes (aunque la denominación
original se refiere exclusivamente a las tres ecuaciones escalares
expresadas en la ecuación (3.72)). Estas ecuaciones son de
carácter muy general, aunque se han deducido adoptando algunas
hipótesis restrictivas (excluyen, por ejemplo, efectos no
newtonianos, de difusión de calor debidos a gradientes de
concentración de especies o de difusión de masa debidos a
gradientes de temperatura3.16), y requerirían ecuaciones
adicionales para describir fenómenos tales como los
electromagnéticos y de radiación térmica, o la generación de calor
y producción y destrucción de especies debidas a reacciones
químicas, como se acaba de indicar. Desafortunadamente, la
resolución de dicho sistema de ecuaciones, aun con dichas
hipótesis simplificadoras, puede ser en general
extraordinariamente complicada y requerir en algunos casos unos
medios informáticos de cálculo no disponibles actualmente.
Subsecciones




Next: Condiciones iniciales y de
Up: Ecuaciones generales de la
Previous: Ecuación de la entropía
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid