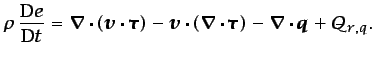Next: Ecuación de conservación de
Up: Forma diferencial
Previous: Forma diferencial
Índice General
La ecuación de conservación de la energía interna se obtiene
restando la ecuación (3.56) de conservación de la
energía mecánica, de la ecuación (3.59) de
conservación de la energía total:
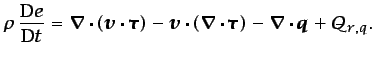 |
(3.60) |
El primer sumando del segundo miembro es el trabajo por unidad de
tiempo que desarrollan las fuerzas de superficie al actuar sobre
la partícula fluida, y el segundo, el trabajo por unidad de tiempo
que ejercerían dichas fuerzas sobre la partícula fluida si ésta se
moviese como un sólido rígido. La diferencia entre ambos es, por
tanto, el trabajo por unidad de tiempo que desarrollan las fuerzas
de superficie al deformar la partícula fluida. Es fácil demostrar
que dicha potencia de deformación puede expresarse de la forma
siguiente:
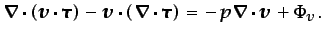 |
(3.61) |
En esta expresión,
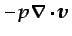 es el trabajo por
unidad de tiempo que realizan las fuerzas de presión al comprimir
la partícula fluida, y es obviamente nulo cuando el fluido se
comporta como incompresible. El término
es el trabajo por
unidad de tiempo que realizan las fuerzas de presión al comprimir
la partícula fluida, y es obviamente nulo cuando el fluido se
comporta como incompresible. El término 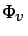 (función de
disipación de Rayleigh) es la potencia que desarrollan las fuerzas
debidas a la viscosidad al deformar la partícula fluida, y puede
demostrarse que es siempre positivo:
(función de
disipación de Rayleigh) es la potencia que desarrollan las fuerzas
debidas a la viscosidad al deformar la partícula fluida, y puede
demostrarse que es siempre positivo:
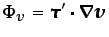 |
(3.62) |
(el producto escalar del tensor de tensiones debidas a la viscosidad por el tensor gradiente del
vector velocidad). Sustituyendo la ecuación (3.61) en
la ecuación (3.60), se obtiene la siguiente expresión
para la ecuación de conservación de la energía interna:
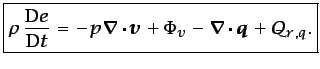 |
(3.63) |
La variación de energía interna de una partícula fluida se debe,
por tanto, al trabajo que realizan las fuerzas de presión al
comprimirla, al trabajo de las fuerzas debidas a la viscosidad al
deformarla, y al calor que recibe la partícula fluida por
conducción, radiación y reacción química. Introduciendo la ley de
Fourier para describir la conducción de calor, la ecuación
(3.63) queda como sigue:
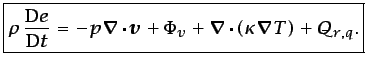 |
(3.64) |




Next: Ecuación de conservación de
Up: Forma diferencial
Previous: Forma diferencial
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid