



Next: Caso multidimensional
Up: Formulación débil
Previous: Formulación débil
Índice General
Se considerará en esta sección la siguiente ecuación diferencial:
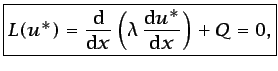 |
(6.28) |
que se satisface en
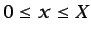 , con las condiciones de
contorno
, con las condiciones de
contorno
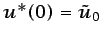 |
(6.29) |
y
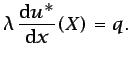 |
(6.30) |
La ecuación (6.28) coincide con la forma estacionaria y unidimensional
de la ecuación (5.44), de la que además se ha
eliminado el término convectivo, y es también equivalente a la
ecuación (5.85) si 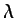 (que sería en este caso la viscosidad del fluido) se
supone uniforme y
(que sería en este caso la viscosidad del fluido) se
supone uniforme y 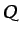 es el gradiente de presión reducida. En
estos dos casos citados, las condiciones de contorno de las
ecuaciones (6.29) y (6.30) equivalen, respectivamente, a fijar la temperatura
o la velocidad en
es el gradiente de presión reducida. En
estos dos casos citados, las condiciones de contorno de las
ecuaciones (6.29) y (6.30) equivalen, respectivamente, a fijar la temperatura
o la velocidad en 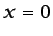 , y un flujo de calor por unidad de área o
una tensión cortante en
, y un flujo de calor por unidad de área o
una tensión cortante en 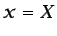 .
.
En muchos problemas no es conveniente utilizar como solución
aproximada una función, como la de la ecuación (6.23), que
satisfaga las condiciones de contorno. Si la solución aproximada
se expresa mediante la ecuación (6.23) con
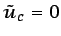 ,
no sólo existirá un residuo de la solución aproximada respecto de
la ecuación en derivadas parciales (6.28), sino también
respecto de las condiciones de contorno. Los residuos
correspondientes a las condiciones de contorno son
,
no sólo existirá un residuo de la solución aproximada respecto de
la ecuación en derivadas parciales (6.28), sino también
respecto de las condiciones de contorno. Los residuos
correspondientes a las condiciones de contorno son
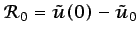 |
(6.31) |
y
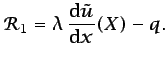 |
(6.32) |
La ecuación equivalente a la ecuación (6.25), en la que se
introducen funciones de ponderación adicionales en el contorno, es
ahora
Dado que el número de grados de libertad de la solución aproximada
de la ecuación (6.23) es 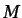 , puede elegirse un número
, puede elegirse un número 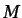 de funciones de ponderación independientes
de funciones de ponderación independientes 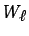 , mientras
que
, mientras
que
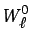 y
y
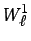 serán dependientes de
serán dependientes de
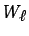 .
.
Para el problema descrito por la ecuación (6.28), la
ecuación (6.33) resulta
![$\displaystyle \int_{0}^{X}W_{\ell}\left[\frac{\mbox{d}}{\mbox{d}x} \left(\lambd...
...W_{\ell}^{1}\left[\lambda \frac{\mbox{d}\tilde{u}}{\mbox{d}x}(X)-{q}\right]=0,$](img916.gif) |
(6.34) |
y las funciones de ponderación en el contorno se reducen a los dos
únicos factores
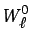 y
y
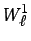 .
.
Integrando por partes el primer término de la ecuación
(6.34), tomando
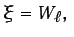
d
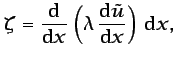
con lo que
d
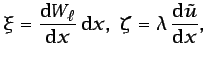
![\begin{displaymath}\begin{split}\left. W_{\ell}\lambda \frac{\mbox{d}\tilde{u}}...
...rac{\mbox{d}\tilde{u}} {\mbox{d}x}(X)-{q}\right]=0. \end{split}\end{displaymath}](img921.gif) |
(6.35) |
Suponiendo que
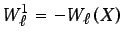 , se obtiene
, se obtiene
![\begin{displaymath}\begin{split}-W_{\ell}(0)\lambda \frac{\mbox{d}\tilde{u}}{\m...
...{0}[\tilde{u}(0)-\tilde{u}_{0}] + W_{\ell}(X){q}=0, \end{split}\end{displaymath}](img923.gif) |
(6.36) |
y si la condición de contorno de tipo Dirichlet puede imponerse
sobre la solución aproximada,
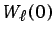 y
y
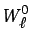 pueden entonces elegirse iguales a cero, de forma que la ecuación
anterior se simplifica, quedando
pueden entonces elegirse iguales a cero, de forma que la ecuación
anterior se simplifica, quedando
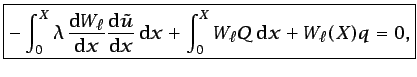 |
(6.37) |
sujeta a las condiciones de contorno
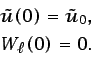 |
(6.38) |
La ecuación (6.37) corresponde a la denominada
formulación débil.




Next: Caso multidimensional
Up: Formulación débil
Previous: Formulación débil
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
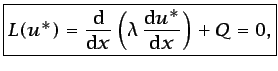
![]() ,
no sólo existirá un residuo de la solución aproximada respecto de
la ecuación en derivadas parciales (6.28), sino también
respecto de las condiciones de contorno. Los residuos
correspondientes a las condiciones de contorno son
,
no sólo existirá un residuo de la solución aproximada respecto de
la ecuación en derivadas parciales (6.28), sino también
respecto de las condiciones de contorno. Los residuos
correspondientes a las condiciones de contorno son
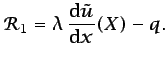
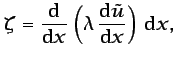
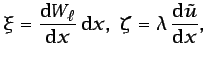
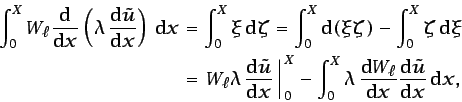
![\begin{displaymath}\begin{split}\left. W_{\ell}\lambda \frac{\mbox{d}\tilde{u}}...
...rac{\mbox{d}\tilde{u}} {\mbox{d}x}(X)-{q}\right]=0. \end{split}\end{displaymath}](img921.gif)
![\begin{displaymath}\begin{split}-W_{\ell}(0)\lambda \frac{\mbox{d}\tilde{u}}{\m...
...{0}[\tilde{u}(0)-\tilde{u}_{0}] + W_{\ell}(X){q}=0, \end{split}\end{displaymath}](img923.gif)