La principal diferencia entre un MRP y los métodos de diferencias
finitas consiste en que en aquéllos se supone que la solución
puede ser representada analíticamente. Consideremos la ecuación en
derivadas parciales para la variable ![]() representada por
representada por
Al sustituir la solución aproximada de la ecuación (6.23) en la ecuación (6.22) se obtiene
| (6.24) |
Cualquier algoritmo de resolución empleado para determinar los
coeficientes ![]() convergerá si permite hacer tender
convergerá si permite hacer tender
![]() a cero, aunque no será posible alcanzar este valor
mediante un número finito de operaciones. En el MRP se trata de
obtener una solución adecuada (definida por el conjunto de los
a cero, aunque no será posible alcanzar este valor
mediante un número finito de operaciones. En el MRP se trata de
obtener una solución adecuada (definida por el conjunto de los ![]() coeficientes
coeficientes ![]() ) imponiendo que un número apropiado de
integrales del residuo ponderado sobre el dominio de cálculo sean
nulas:
) imponiendo que un número apropiado de
integrales del residuo ponderado sobre el dominio de cálculo sean
nulas:
Los distintos métodos que pertenecen a esta clase de métodos de
residuos ponderados se obtienen eligiendo diferentes funciones de
pesado ![]() (Fletcher, 1991).
(Fletcher, 1991).
En el método de los subdominios, el dominio de cálculo se divide
en ![]() subdominios
subdominios ![]() , siendo
, siendo
![]() en
en ![]() y
y
![]() fuera de
fuera de ![]() . Este método evalúa la integral
de la ecuación (6.25) del mismo modo empleado en el método
de volúmenes finitos.
. Este método evalúa la integral
de la ecuación (6.25) del mismo modo empleado en el método
de volúmenes finitos.
En el método de colocación,
![]() , siendo
, siendo ![]() la delta de
Dirac y
la delta de
Dirac y
![]() . A partir de la ecuación
(6.25) se deduce que este método es equivalente a hacer
. A partir de la ecuación
(6.25) se deduce que este método es equivalente a hacer
![]() , lo que recuerda a los
métodos de
diferencias finitas, con la distinción de que en éstos no se
utilizan funciones de aproximación.
, lo que recuerda a los
métodos de
diferencias finitas, con la distinción de que en éstos no se
utilizan funciones de aproximación.
En el método de mínimos cuadrados se toma
![]() , con lo que la ecuación
(6.25) resulta equivalente a la condición de que
, con lo que la ecuación
(6.25) resulta equivalente a la condición de que
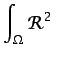 d d |
(6.26) |
En el método de residuos ponderados de Galerkin, las
funciones de ponderación se toman iguales a las funciones de
aproximación,
![]() . Si
las funciones de aproximación forman un conjunto completo, la
ecuación (6.25) expresa que el residuo es ortogonal a
cualquier elemento del conjunto, por lo que, si se hace tender
. Si
las funciones de aproximación forman un conjunto completo, la
ecuación (6.25) expresa que el residuo es ortogonal a
cualquier elemento del conjunto, por lo que, si se hace tender ![]() a infinito, la solución aproximada,
a infinito, la solución aproximada, ![]() , convergerá a la
solución exacta,
, convergerá a la
solución exacta, ![]() . Si se eligen, por ejemplo, polinomios
como funciones de aproximación, un conjunto completo sería el
siguiente:
. Si se eligen, por ejemplo, polinomios
como funciones de aproximación, un conjunto completo sería el
siguiente:
![]() .
.
Obsérvese que por el momento no se está haciendo referencia
directamente al método de los elementos finitos (MEF) de Galerkin,
que será descrito en el siguiente capítulo como un caso particular
del método de Galerkin de residuos ponderados que se acaba de
describir. Antes de ello, vamos a hacer una breve referencia al
método espectral de Galerkin, y a comentar su relación con el
método de los residuos ponderados de Galerkin. El método
espectral, a diferencia de los métodos de diferencias finitas,
volúmenes finitos y elementos finitos, que son de tipo local, es
de carácter global. Como en el método de residuos ponderados de
Galerkin antes descrito, en el método espectral las funciones de
aproximación y de ponderación son no nulas sobre todo el dominio
de cálculo; por el contrario, el método de los elementos finitos,
que, como se verá a continuación, identifica los coeficientes
![]() con las incógnitas en los nodos de una malla de
cálculo, es de carácter local. La principal diferencia del método
espectral con el MRP de Galerkin consiste en que aquél utiliza
funciones de aproximación y de ponderación ortogonales (series de
Fourier, polinomios de Legendre, etc.):
con las incógnitas en los nodos de una malla de
cálculo, es de carácter local. La principal diferencia del método
espectral con el MRP de Galerkin consiste en que aquél utiliza
funciones de aproximación y de ponderación ortogonales (series de
Fourier, polinomios de Legendre, etc.):
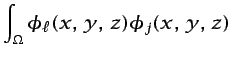 d d |
|||
| (6.27) |