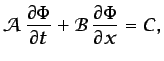 |
(6.1) |
Las propiedades matemáticas de las diferentes ecuaciones de conservación que se han presentado en los capítulos anteriores obviamente están estrechamente relacionadas con las características físicas de los distintos tipos de flujos que describen. El carácter parabólico, hiperbólico o elíptico de las ecuaciones aproximadas depende del carácter de los distintos términos que aparecen en ellas.
La clasificación de las ecuaciones diferenciales en derivadas parciales puede hacerse utilizando el concepto matemático de superficies características. Consideraremos en lo que sigue, para simplificar la discusión, problemas descritos por ecuaciones diferenciales en derivadas parciales en las que sólo intervienen dos variables independientes (el tiempo y una coordenada espacial en problemas no estacionarios, o dos coordenadas espaciales en problemas estacionarios). En estos problemas, en la integración a lo largo de las líneas características (cuando éstas existen) de las ecuaciones que describen el flujo sólo intervienen diferenciales totales. Esto es lo que precisamente define a las líneas características, a lo largo de las cuales se verifican unas relaciones de compatibilidad que representan una formulación alternativa al sistema de ecuaciones original.
Veamos el ejemplo sencillo de una ecuación hiperbólica de primer orden,
Consideremos ahora una ecuación de segundo orden. El carácter de una ecuación viene determinado por los coeficientes de las derivadas de mayor orden, por lo que consideraremos una ecuación expresada de la forma siguiente:
El discriminante
![]() determina el número de soluciones para la pendiente
d
determina el número de soluciones para la pendiente
d![]() d
d![]() que satisfacen la ecuación (6.9) en cada punto, y que, por
tanto, definen las direcciones características a lo largo de las
cuales se satisface y puede integrarse la ecuación (6.10).
que satisfacen la ecuación (6.9) en cada punto, y que, por
tanto, definen las direcciones características a lo largo de las
cuales se satisface y puede integrarse la ecuación (6.10).
Si
![]() , existirán dos
soluciones reales de la ecuación (6.9) y, por tanto, dos líneas
características reales, a lo largo de las cuales se satisface la
relación de la ecuación (6.10). Se dice entonces que la ecuación tiene
un carácter hiperbólico. Veremos a continuación que las ecuaciones
en derivadas parciales hiperbólicas están asociadas con problemas
de propagación de ondas en los que no existen procesos
disipativos, lo que determina que si las condiciones iniciales o
de contorno contienen discontinuidades, éstas se propagarán en el
interior del dominio. Esto es consistente con la posibilidad de
que en las características existan discontinuidades en las
derivadas normales de las magnitudes fluidas (las derivadas
tangenciales son continuas). El hecho de que la ecuación (6.5) pueda
resolverse mediante la integración de la ecuación (6.10) a lo largo de
las características reales que existen en problemas hiperbólicos
indica que la información se propaga en dichos problemas a lo
largo de éstas. La solución en el segmento de línea AB de la
Figura 6.1 (que no coincide con una característica) se
propagará a lo largo de las características que parten de AB.
, existirán dos
soluciones reales de la ecuación (6.9) y, por tanto, dos líneas
características reales, a lo largo de las cuales se satisface la
relación de la ecuación (6.10). Se dice entonces que la ecuación tiene
un carácter hiperbólico. Veremos a continuación que las ecuaciones
en derivadas parciales hiperbólicas están asociadas con problemas
de propagación de ondas en los que no existen procesos
disipativos, lo que determina que si las condiciones iniciales o
de contorno contienen discontinuidades, éstas se propagarán en el
interior del dominio. Esto es consistente con la posibilidad de
que en las características existan discontinuidades en las
derivadas normales de las magnitudes fluidas (las derivadas
tangenciales son continuas). El hecho de que la ecuación (6.5) pueda
resolverse mediante la integración de la ecuación (6.10) a lo largo de
las características reales que existen en problemas hiperbólicos
indica que la información se propaga en dichos problemas a lo
largo de éstas. La solución en el segmento de línea AB de la
Figura 6.1 (que no coincide con una característica) se
propagará a lo largo de las características que parten de AB.
Si
![]() , existirá una
única línea característica real, y la ecuación correspondiente
tiene carácter parabólico. La característica a través de un punto
P divide las zonas de dependencia e influencia de dicho punto.
Puede argumentarse que la información se propaga a velocidad
infinita, por lo que, en un problema no estacionario
unidimensional, por ejemplo, cualquier perturbación introducida en
un punto P en un instante dado
, existirá una
única línea característica real, y la ecuación correspondiente
tiene carácter parabólico. La característica a través de un punto
P divide las zonas de dependencia e influencia de dicho punto.
Puede argumentarse que la información se propaga a velocidad
infinita, por lo que, en un problema no estacionario
unidimensional, por ejemplo, cualquier perturbación introducida en
un punto P en un instante dado ![]() puede afectar a la solución
en todos los puntos del dominio en
puede afectar a la solución
en todos los puntos del dominio en ![]() , si bien la
influencia será progresivamente menor en puntos cada vez más
alejados de P. En problemas estacionarios bidimensionales, las
características serán perpendiculares a la dirección del flujo y
cualquier perturbación del flujo en un punto P no tendrá
influencia aguas arriba de P. Obviamente, las características no
desempeñan en estos flujos el papel que juegan en problemas
parabólicos, y utilizar una malla de cálculo basada en las
características no permitiría avanzar en el tiempo o en la
dirección predominante del flujo para determinar la solución. En
contraste con lo que ocurre en ecuaciones hiperbólicas, las
derivadas de la variable dependiente
, si bien la
influencia será progresivamente menor en puntos cada vez más
alejados de P. En problemas estacionarios bidimensionales, las
características serán perpendiculares a la dirección del flujo y
cualquier perturbación del flujo en un punto P no tendrá
influencia aguas arriba de P. Obviamente, las características no
desempeñan en estos flujos el papel que juegan en problemas
parabólicos, y utilizar una malla de cálculo basada en las
características no permitiría avanzar en el tiempo o en la
dirección predominante del flujo para determinar la solución. En
contraste con lo que ocurre en ecuaciones hiperbólicas, las
derivadas de la variable dependiente ![]() son siempre continuas
en las características, y, debido a la presencia de mecanismos
disipativos, ninguna discontinuidad que pueda existir en las
condiciones iniciales o de contorno persistirá en el interior del
dominio de cálculo.
son siempre continuas
en las características, y, debido a la presencia de mecanismos
disipativos, ninguna discontinuidad que pueda existir en las
condiciones iniciales o de contorno persistirá en el interior del
dominio de cálculo.
Si
![]() , no existirá
ninguna característica real, y la ecuación correspondiente tiene
carácter elíptico. En este caso, cualquier perturbación
introducida en un punto P del dominio de cálculo afectará a la
solución en cualquier otro punto, si bien de nuevo la influencia
será pequeña en puntos alejados. Mientras que en flujos
parabólicos e hiperbólicos es posible utilizar un procedimiento de
avance en el tiempo o a lo largo de la dirección del flujo a
partir de las condiciones ``iniciales'', en problemas elípticos
esto no es posible. Cualquier discontinuidad que pueda existir en
el contorno es suavizada en el interior del dominio debido a los
mecanismos disipativos.
, no existirá
ninguna característica real, y la ecuación correspondiente tiene
carácter elíptico. En este caso, cualquier perturbación
introducida en un punto P del dominio de cálculo afectará a la
solución en cualquier otro punto, si bien de nuevo la influencia
será pequeña en puntos alejados. Mientras que en flujos
parabólicos e hiperbólicos es posible utilizar un procedimiento de
avance en el tiempo o a lo largo de la dirección del flujo a
partir de las condiciones ``iniciales'', en problemas elípticos
esto no es posible. Cualquier discontinuidad que pueda existir en
el contorno es suavizada en el interior del dominio debido a los
mecanismos disipativos.
Un sistema de ecuaciones puede contener ecuaciones de distinto tipo. Por otra parte, también es posible definir el carácter de una ecuación con respecto a direcciones particulares.
Comentaremos a continuación algunos ejemplos de ecuaciones de distinto carácter que aparecen en mecánica de fluidos.