



Next: Ecuaciones de Navier-Stokes en
Up: Aplicación del MEF a
Previous: Flujos potenciales
Índice General
Problemas de convección-difusión
Se va a considerar en esta sección un problema descrito por la
ecuación (5.44) de conservación de la energía interna para
flujos incompresibles,
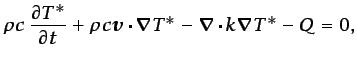 |
(6.59) |
con las condiciones de contorno
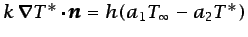 |
(6.60) |
en una parte del contorno
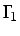 , y
, y
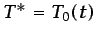 |
(6.61) |
en el contorno
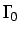 , y con la condición inicial
, y con la condición inicial
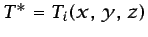 |
(6.62) |
en 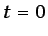 . Se considera que la conductividad térmica y el calor
específico pueden ser variables con la temperatura. Los parámetros
. Se considera que la conductividad térmica y el calor
específico pueden ser variables con la temperatura. Los parámetros
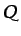 y
y 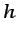 pueden especificarse de forma arbitraria. La
distribución de velocidad
pueden especificarse de forma arbitraria. La
distribución de velocidad 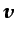 se considera también conocida.
La ecuación (6.59) podría describir asimismo la
conservación de especies o de otro escalar.
se considera también conocida.
La ecuación (6.59) podría describir asimismo la
conservación de especies o de otro escalar.
En cada elemento, se supone que la distribución de temperatura
puede aproximarse mediante
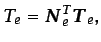 |
(6.63) |
donde
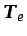 contiene las temperaturas en los nodos del
elemento y
contiene las temperaturas en los nodos del
elemento y
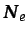 es un vector de funciones de forma:
es un vector de funciones de forma:
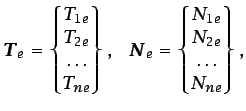 |
(6.64) |
siendo 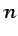 el número de nodos por elemento. La derivada temporal
es
el número de nodos por elemento. La derivada temporal
es
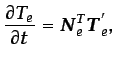 |
(6.65) |
siendo
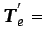 d
d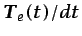 .
.
La expresión equivalente a la ecuación (6.42), resultante
de la aplicación de la formulación del método de los residuos
ponderados de Galerkin, es en este caso
![\begin{displaymath}\begin{split}S_{e}\left[\int_{\Omega_{e}}\vec{N}_{e}\rho c_{e...
...h_{e}a_{1}T_{\infty} \mbox{d}\Gamma\right]=\{0\}, \end{split}\end{displaymath}](img991.gif) |
(6.66) |
donde 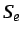 es un operador Booleano que almacena las
contribuciones de la matrices elementales en las matrices
globales.
es un operador Booleano que almacena las
contribuciones de la matrices elementales en las matrices
globales.
Debe recordarse que la condición expresada en la
ecuación (6.60) es válida para representar, por ejemplo,
tanto condiciones de contorno convectivas (
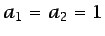 ) como
de flujo de calor constante (
) como
de flujo de calor constante (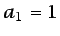 ,
, 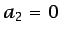 ). Las integrales
de la ecuación (6.66) extendidas al contorno puede por tanto aplicarse,
con los valores apropiados de los parámetros
). Las integrales
de la ecuación (6.66) extendidas al contorno puede por tanto aplicarse,
con los valores apropiados de los parámetros 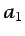 y
y 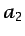 , a
distintas partes del contorno, según sea necesario.
, a
distintas partes del contorno, según sea necesario.
Debe observarse que la ecuación (6.66) constituye un sistema
de ecuaciones diferenciales ordinarias que permite determinar la
evolución temporal de la temperatura en los nodos. En el caso de
que el problema fuese estacionario, se obtiene un sistema de
ecuaciones algebraicas no lineales que proporciona la distribución
de temperaturas en los nodos.
La ecuación (6.66) puede escribirse de la forma siguiente:
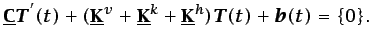 |
(6.67) |
Las condiciones de contorno de tipo Dirichlet deben tenerse en
cuenta como se ha indicado anteriormente.
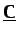 es la matriz
de capacidad térmica,
es la matriz
de capacidad térmica,
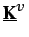 es una matriz no simétrica que
procede del término de convección en la ecuación diferencial,
es una matriz no simétrica que
procede del término de convección en la ecuación diferencial,
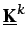 procede del término de difusión,
procede del término de difusión,
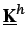 contiene parte de la contribución de las condiciones de contorno
convectivas (término homogéneo) y
contiene parte de la contribución de las condiciones de contorno
convectivas (término homogéneo) y
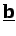 es el vector flujo de
calor (contribuciones procedentes de condiciones de contorno y de
términos fuente en las ecuaciones). También se incluyen en
es el vector flujo de
calor (contribuciones procedentes de condiciones de contorno y de
términos fuente en las ecuaciones). También se incluyen en
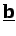 contribuciones procedentes de nodos del contorno donde
se aplican condiciones de contorno de tipo Dirichlet, como
resultado de la partición que debe hacerse para igualar el número
de ecuaciones al de incógnitas contenidas en
contribuciones procedentes de nodos del contorno donde
se aplican condiciones de contorno de tipo Dirichlet, como
resultado de la partición que debe hacerse para igualar el número
de ecuaciones al de incógnitas contenidas en 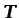 .
.




Next: Ecuaciones de Navier-Stokes en
Up: Aplicación del MEF a
Previous: Flujos potenciales
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
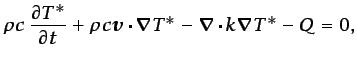
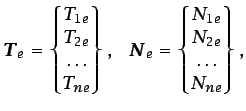
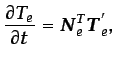
![]() ) como
de flujo de calor constante (
) como
de flujo de calor constante (![]() ,
, ![]() ). Las integrales
de la ecuación (6.66) extendidas al contorno puede por tanto aplicarse,
con los valores apropiados de los parámetros
). Las integrales
de la ecuación (6.66) extendidas al contorno puede por tanto aplicarse,
con los valores apropiados de los parámetros ![]() y
y ![]() , a
distintas partes del contorno, según sea necesario.
, a
distintas partes del contorno, según sea necesario.