



Next: Bibliografía
Up: Aplicación del MEF a
Previous: Problemas de convección-difusión
Índice General
Se van a discutir en esta sección algunos aspectos de la
aplicación del MEF a un problema descrito por las ecuaciones
estacionarias de Navier-Stokes para flujos incompresibles de
fluidos con viscosidad constante. Como ya se comentó
anteriormente, en este tipo de flujo las ecuaciones de
conservación de la masa y de la cantidad de movimiento están
desacopladas de la ecuación de conservación de la energía, por lo
que en lo que sigue se considerarán sólo las dos primeras. La
ecuación de conservación de la energía podría resolverse a
continuación, una vez conocida la distribución de velocidad en el
flujo. Las ecuaciones a resolver son, por tanto, las ecuaciones
(5.38) a (5.39):
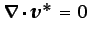 |
(6.68) |
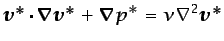 |
(6.69) |
(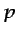 se supondrá que es una presión reducida).
se supondrá que es una presión reducida).
Utilizando una función de ponderación 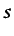 asociada a la ecuación
(6.68) y otra función vectorial
asociada a la ecuación
(6.68) y otra función vectorial 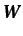 asociada a la ecuación
(6.69), la formulación de residuos ponderados puede
escribirse de la forma
asociada a la ecuación
(6.69), la formulación de residuos ponderados puede
escribirse de la forma
Integrando por partes los términos segundo y cuarto de esta
ecuación, se obtiene
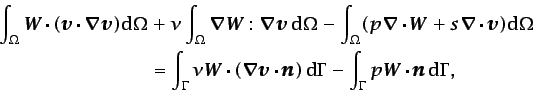 |
(6.71) |
siendo 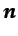 el vector unitario normal al contorno.
el vector unitario normal al contorno.
Los términos del segundo miembro de la ecuación (6.71) para
un problema bidimensional pueden ponerse de la forma
![$\displaystyle \int_{\Gamma}[\nu W_{x}(\vec{\nabla}u\cdot\vec{n}) + \nu W_{y}(\vec{\nabla}v\cdot\vec{n})-p(W_{x}n_{x}+W_{y}n_{y})]$](img1014.gif) d d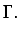 |
(6.72) |
Las condiciones de contorno para un problema correspondiente a un
flujo interno en un conducto de forma arbitraria, por ejemplo,
para el que se utiliza un dominio de cálculo limitado por las
paredes del conducto y por las secciones de entrada y salida,
serán las siguientes:
- En las paredes se impone la condición de no deslizamiento:
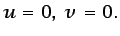 |
(6.73) |
- En la sección de entrada se impone una determinada
distribución de velocidad. Suponiendo que el flujo entra sólo con
componente
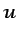 , las condiciones son:
, las condiciones son:
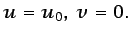 |
(6.74) |
Tanto estas condiciones como las anteriores son obviamente
condiciones de contorno esenciales.
- En la sección de salida
(suponiendo que ésta es perpendicular al eje
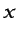 y que, por tanto,
y que, por tanto,
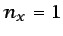 y
y 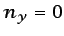 ), los términos del segundo miembro de la
ecuación (6.71) toman la forma
), los términos del segundo miembro de la
ecuación (6.71) toman la forma
![$\displaystyle \int_{\Gamma}\left[-pW_{x}+\nu\left(W_{x} \frac{\partial u}{\partial x}+W_{y} \frac{\partial v}{\partial x}\right)\right]$](img1020.gif) d d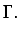 |
(6.75) |
Si se comparan estos términos con los correspondientes de la
ecuación (6.37), se observa que como condiciones de contorno
naturales pueden imponerse valores de las magnitudes
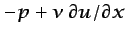 y
y
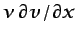 . Si
se los gradientes de
. Si
se los gradientes de 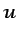 y
y 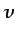 según
según 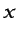 pueden suponerse
despreciables en la sección de salida, lo que suele ser aceptable,
y se tiene en cuenta que la presión tan sólo aparece en las
ecuaciones en el término
pueden suponerse
despreciables en la sección de salida, lo que suele ser aceptable,
y se tiene en cuenta que la presión tan sólo aparece en las
ecuaciones en el término
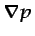 , de forma que la solución
para la distribución de presiones satisface las ecuaciones si se
le suma una constante, se deduce que pueden imponerse valores
nulos para las magnitudes mencionadas. De esta forma, los términos
del segundo miembro de la ecuación (6.71) pueden
despreciarse.
, de forma que la solución
para la distribución de presiones satisface las ecuaciones si se
le suma una constante, se deduce que pueden imponerse valores
nulos para las magnitudes mencionadas. De esta forma, los términos
del segundo miembro de la ecuación (6.71) pueden
despreciarse.
Dado que la presión no interviene en la ecuación (6.71)
dentro de una derivada, a diferencia de lo que ocurre con las
componentes de la velocidad, cuyas derivadas primeras sí aparecen,
parece razonable elegir diferentes funciones de forma para la
presión y las componentes de la velocidad. Introduciendo las
funciones de forma en la ecuación (6.71) se obtiene el
sistema de ecuaciones
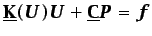 |
(6.76) |
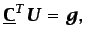 |
(6.77) |
donde 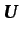 es el vector de componentes de la velocidad en los
nodos,
es el vector de componentes de la velocidad en los
nodos, 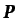 el vector de presiones en los nodos,
el vector de presiones en los nodos, 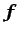 y
y
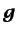 vectores que incorporan las condiciones de contorno,
vectores que incorporan las condiciones de contorno,
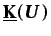 una matriz simétrica definida positiva, y
una matriz simétrica definida positiva, y
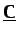 una matriz asimétrica indefinida. Debido al carácter
indefinido de la matriz
una matriz asimétrica indefinida. Debido al carácter
indefinido de la matriz
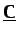 , es posible, por ejemplo, que
para
, es posible, por ejemplo, que
para 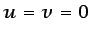 ,
, 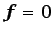 y
y 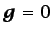 , la ecuación
, la ecuación
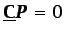 permita soluciones no triviales para
permita soluciones no triviales para 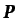 .
Para evitar problemas de este tipo se recurre a utilizar una
interpolación mixta, empleando esquemas de interpolación
diferentes para las componentes de la velocidad y de la presión.
Al ser inferiores las condiciones de regularidad para la presión
que para la velocidad, la presión se aproxima mediante polinomios
de interpolación de un grado más bajo que los utilizados para la
velocidad.
.
Para evitar problemas de este tipo se recurre a utilizar una
interpolación mixta, empleando esquemas de interpolación
diferentes para las componentes de la velocidad y de la presión.
Al ser inferiores las condiciones de regularidad para la presión
que para la velocidad, la presión se aproxima mediante polinomios
de interpolación de un grado más bajo que los utilizados para la
velocidad.
En cuanto al tipo de elementos empleados para este problema,
suelen preferirse elementos triangulares con siete grados de
libertad para las componentes de la velocidad y tres grados de
libertad para la presión, o bien cuadriláteros con nueve y tres
grados de libertad para componentes de la velocidad y presión
respectivamente. Puede consultarse el texto de Cuvelier et al. (1986) indicado en la bibliografía donde se discute la elección de
los elementos.
Por último, cabe indicar que la resolución de los sistemas
(6.76) y (6.77) no es sencilla al contener la matriz
correspondiente ceros en la diagonal. Para facilitar la resolución
se suele hacer uso del método de penalización, ya mencionado en
otras asignaturas. Una revisión sobre el uso del método de los
elementos finitos en flujos incompresibles viscosos puede
encontrase en la publicación de Gresho (1989) indicada en la
bibliografía.




Next: Bibliografía
Up: Aplicación del MEF a
Previous: Problemas de convección-difusión
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![]() asociada a la ecuación
(6.68) y otra función vectorial
asociada a la ecuación
(6.68) y otra función vectorial ![]() asociada a la ecuación
(6.69), la formulación de residuos ponderados puede
escribirse de la forma
asociada a la ecuación
(6.69), la formulación de residuos ponderados puede
escribirse de la forma
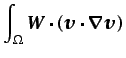 d
d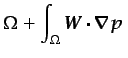 d
d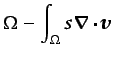 d
d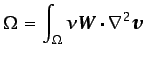 d
d![$\displaystyle \int_{\Gamma}[\nu W_{x}(\vec{\nabla}u\cdot\vec{n}) + \nu W_{y}(\vec{\nabla}v\cdot\vec{n})-p(W_{x}n_{x}+W_{y}n_{y})]$](img1014.gif) d
d![$\displaystyle \int_{\Gamma}\left[-pW_{x}+\nu\left(W_{x} \frac{\partial u}{\partial x}+W_{y} \frac{\partial v}{\partial x}\right)\right]$](img1020.gif) d
d