



Next: Problemas de convección-difusión
Up: Aplicación del MEF a
Previous: Aplicación del MEF a
Índice General
Consideraremos un flujo potencial y estacionario de un fluido
incompresible en el interior de un conducto, en el que se halla
inmerso un cuerpo fuselado. El flujo quedará descrito por la
distribución del potencial de velocidad 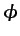 , que satisface la
ecuación (5.9),
, que satisface la
ecuación (5.9),
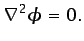 |
(6.54) |
El problema es obviamente elíptico. Las componentes de la
velocidad se obtienen a partir de la distribución de 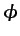 mediante la ecuación (5.7),
mediante la ecuación (5.7),
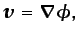 |
(6.55) |
Las condiciones de contorno pueden ser de tipo Dirichlet en los
contornos de flujo entrante y de flujo saliente y de tipo Neumann
en las paredes interiores del conducto y del cuerpo
(
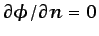 ), siendo
), siendo 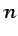 la normal a la pared, lo que
equivale a imponer que las paredes son impermeables. Por ejemplo,
fijar un valor uniforme de
la normal a la pared, lo que
equivale a imponer que las paredes son impermeables. Por ejemplo,
fijar un valor uniforme de 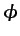 en cada uno de los contornos de
entrada y salida, al ser en tal caso
en cada uno de los contornos de
entrada y salida, al ser en tal caso
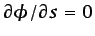 , siendo
, siendo 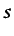 la tangente al contorno, equivale a imponer que la velocidad es
normal al contorno. El caudal a través del conducto vendrá
determinado por la diferencia entre los valores de
la tangente al contorno, equivale a imponer que la velocidad es
normal al contorno. El caudal a través del conducto vendrá
determinado por la diferencia entre los valores de 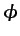 impuestos en dichos contornos de entrada y salida. También sería
posible fijar
impuestos en dichos contornos de entrada y salida. También sería
posible fijar
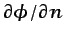 en uno de estos contornos (el de
entrada o el de salida), lo que equivaldría a fijar la velocidad
normal a éste.
en uno de estos contornos (el de
entrada o el de salida), lo que equivaldría a fijar la velocidad
normal a éste.
La formulación débil equivalente a la de la ecuación (6.42) es en este
caso
Introduciendo
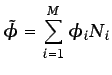 |
(6.57) |
en la ecuación (6.56), se obtiene




Next: Problemas de convección-difusión
Up: Aplicación del MEF a
Previous: Aplicación del MEF a
Índice General
© 2000, 2001, Julio Hernández Rodríguez, ETSII, Universidad Nacional de Educación a Distancia, Madrid
![]() , que satisface la
ecuación (5.9),
, que satisface la
ecuación (5.9),